题目内容
(2011•金华)某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

解:(1)设师生返校时的函数解析式为s=kt+b,
如图所示,把(12,8)、(13,3)代入上式中得,
 解此方程组得,
解此方程组得,

∴s=﹣5t+68,
当s=0时,t=13.6,
t=13时36分
∴师生在13时36分回到学校;
(2)该三轮车运送树苗时,离校路程s与时间t之间的图象如图所示:

由图象得,当三轮车追上师生时,离学校4km;
(3)设符合学校要求的植树点与学校的路程为x(km),
由题意得: <14,解得,
<14,解得,
x< ,
,
答:A、B、C植树点符合学校的要求.
如图所示,把(12,8)、(13,3)代入上式中得,
 解此方程组得,
解此方程组得,
∴s=﹣5t+68,
当s=0时,t=13.6,
t=13时36分
∴师生在13时36分回到学校;
(2)该三轮车运送树苗时,离校路程s与时间t之间的图象如图所示:

由图象得,当三轮车追上师生时,离学校4km;
(3)设符合学校要求的植树点与学校的路程为x(km),
由题意得:
 <14,解得,
<14,解得,x<
 ,
,答:A、B、C植树点符合学校的要求.
略

练习册系列答案
相关题目
 ,求此时直线PM的解析式;
,求此时直线PM的解析式; ,PM的延长线与CD的延长线交于点F,若三角形G
,PM的延长线与CD的延长线交于点F,若三角形G
 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
 时,
时,
 不经过第 象限.
不经过第 象限.
 ,
, 是一次函数
是一次函数 的图像和反比例函数
的图像和反比例函数 的
的
 与
与 轴的交点
轴的交点 的坐标及
的坐标及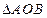 的面积.
的面积. 动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为
动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为 (棵),乙班植树的总量为
(棵),乙班植树的总量为 (棵),两班一起植树所用的时间(从甲班开始植树时计时)为
(棵),两班一起植树所用的时间(从甲班开始植树时计时)为 (时),
(时), 所示.
所示.
 时,甲、乙两班植树的总量之和能否超过
时,甲、乙两班植树的总量之和能否超过 棵.
棵.