题目内容
如图,在⊙O中,弦AB∥弦CD,且分居在点O的两侧.已知AB=11,CD=21,⊙O的半径R=
.求:

(1)AB与CD之间的距离.
(2)若⊙I1、⊙I2分别为△ACD、△ABC的内切圆,求⊙I1、⊙I2的半径之比.
| 65 |
| 6 |

(1)AB与CD之间的距离.
(2)若⊙I1、⊙I2分别为△ACD、△ABC的内切圆,求⊙I1、⊙I2的半径之比.
考点:三角形的内切圆与内心,勾股定理,垂径定理
专题:
分析:(1)分别作弦AB、CD的弦心距,设垂足为E、F;由于AB∥CD,则E、O、F三点共线,EF即为AB、CD间的距离;由垂径定理,易求得AE、DF的长,连接OA、OD,在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离;
(2)先证明四边形ABCD是等腰梯形,作等腰梯形ABCD的高AE,BF,运用勾股定理求出AD=13,AC=20,运用梯形的面积公式得出S梯形ABCD=192,则S△ADC=126,S△ABC=66,然后由面积法分别求出⊙I1的半径r1=
,⊙I2的半径r2=3,则⊙I1与⊙I2的半径之比可求.
(2)先证明四边形ABCD是等腰梯形,作等腰梯形ABCD的高AE,BF,运用勾股定理求出AD=13,AC=20,运用梯形的面积公式得出S梯形ABCD=192,则S△ADC=126,S△ABC=66,然后由面积法分别求出⊙I1的半径r1=
| 14 |
| 3 |
解答: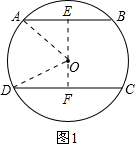 解:(1)如图1,过O作OE⊥AB于点E,OF⊥CD于点F,连接OA,OD.
解:(1)如图1,过O作OE⊥AB于点E,OF⊥CD于点F,连接OA,OD.
∵AB∥CD,∴E,O,F三点共线,
∴EF即为所求的AB,CD的距离
∴AE=
AB=
,DF=
CD=
,
在Rt△OAE中,∵OB=
,AE=
,∴OE=
.
在Rt△ODF中,∵OD=
,DF=
,∴OF=
,
∴EF=OE+OF=
+
=12,
答:AB和CD的距离为12;
 (2)∵AB∥CD,AB≠CD,
(2)∵AB∥CD,AB≠CD,
∴四边形ABCD是梯形,
∵在⊙O中,弦AB∥弦CD,
∴
=
,
∴AD=BC,
∴梯形ABCD是等腰梯形.
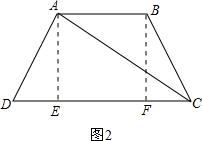
如图2,作等腰梯形ABCD的高AE,BF,则四边形ABFE是矩形,FE=AB=11,DE=CF=
=5.
在△ADE中,∵∠AED=90°,
∴AD=
=
=13,
在△ACE中,∵∠AEC=90°,
∴AC=
=
=20.
S梯形ABCD=
(AB+CD)•EF=
(11+21)×12=192,
∵S△ADC+S△ABC=192,S△ADC:S△ABC=21:11,
∴S△ADC=126,S△ABC=66.
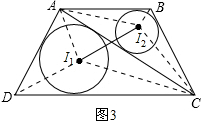 如图3,连接I1A、I1D、I1C,设△ACD的内切圆半径为r1,
如图3,连接I1A、I1D、I1C,设△ACD的内切圆半径为r1,
∵S△ADC=S△AI1D+S△DI1C+S△AI1C=
AD•r1+
CD•r1+
CA•r1,
∴
(13+21+20)r1=126,
∴r1=
,
同理,求出⊙I2的半径r2=3,
∴⊙I1与⊙I2的半径之比是
:3=
.
 解:(1)如图1,过O作OE⊥AB于点E,OF⊥CD于点F,连接OA,OD.
解:(1)如图1,过O作OE⊥AB于点E,OF⊥CD于点F,连接OA,OD.∵AB∥CD,∴E,O,F三点共线,
∴EF即为所求的AB,CD的距离
∴AE=
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
| 21 |
| 2 |
在Rt△OAE中,∵OB=
| 65 |
| 6 |
| 11 |
| 2 |
| 28 |
| 3 |
在Rt△ODF中,∵OD=
| 65 |
| 6 |
| 21 |
| 2 |
| 8 |
| 3 |
∴EF=OE+OF=
| 28 |
| 3 |
| 8 |
| 3 |
答:AB和CD的距离为12;
 (2)∵AB∥CD,AB≠CD,
(2)∵AB∥CD,AB≠CD,∴四边形ABCD是梯形,
∵在⊙O中,弦AB∥弦CD,
∴
 |
| AD |
 |
| BC |
∴AD=BC,
∴梯形ABCD是等腰梯形.
如图2,作等腰梯形ABCD的高AE,BF,则四边形ABFE是矩形,FE=AB=11,DE=CF=
| CD-AB |
| 2 |
在△ADE中,∵∠AED=90°,
∴AD=
| DE2+AE2 |
| 52+122 |
在△ACE中,∵∠AEC=90°,
∴AC=
| EC2+AE2 |
| 162+122 |
S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ADC+S△ABC=192,S△ADC:S△ABC=21:11,
∴S△ADC=126,S△ABC=66.
 如图3,连接I1A、I1D、I1C,设△ACD的内切圆半径为r1,
如图3,连接I1A、I1D、I1C,设△ACD的内切圆半径为r1,∵S△ADC=S△AI1D+S△DI1C+S△AI1C=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴r1=
| 14 |
| 3 |
同理,求出⊙I2的半径r2=3,
∴⊙I1与⊙I2的半径之比是
| 14 |
| 3 |
| 14 |
| 9 |
点评:本题考查了等腰梯形的判定与性质,垂径定理,勾股定理,三角形的内切圆,三角形、梯形的面积,综合性较强,有一定难度.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,四边形ABCD内接于⊙O,∠BOD=130°,则∠BCD的度数为( )
如图,四边形ABCD内接于⊙O,∠BOD=130°,则∠BCD的度数为( )| A、50° | B、125° |
| C、115° | D、150° |
宁波市是国家优秀旅游城市,吸引了众多的海内外游客.据宁波市2012年国民经济和社会发展统计公报显示,全年旅游总收入达862.8亿元.将862.8亿元用科学记数法可表示为( )
| A、86.28×109元 |
| B、86.28×1010元 |
| C、8.628×1010元 |
| D、8.628×1011元 |
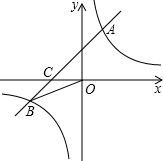 已知,如图,在平面直角坐标系中,直线y=x+b与双曲线
已知,如图,在平面直角坐标系中,直线y=x+b与双曲线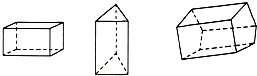 如图,至少找出下列几何体的4个共同点.
如图,至少找出下列几何体的4个共同点. 如图,点A、B、C在半径为3的⊙O上,∠A=40°,则扇形OBC(图中阴影部分)的面积等于
如图,点A、B、C在半径为3的⊙O上,∠A=40°,则扇形OBC(图中阴影部分)的面积等于 如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为
如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为