题目内容
26、如图,半径分别为4cm和3cm的⊙O1,⊙O2相交于A,B两点,且O1O2=6cm,过点A作⊙O1的弦AC与⊙O2相切,作⊙O2的弦AD与⊙O1相切.
(1)求证:AB2=BC•BD;
(2)两圆同时沿连心线都以每秒1cm的速度相向移动,几秒钟时,两圆相切?
(3)在(2)的条件下,三点B,C,D能否在同一直线上?若能,求出移动的时间;若不能,说明理由.
(1)求证:AB2=BC•BD;
(2)两圆同时沿连心线都以每秒1cm的速度相向移动,几秒钟时,两圆相切?
(3)在(2)的条件下,三点B,C,D能否在同一直线上?若能,求出移动的时间;若不能,说明理由.

分析:(1)由弦切角定理知,∠CAB=∠D,∠DAB=∠C,故有△ABC∽△DBA,有AB:BD=BC:AB,即AB2=BC•BD;
(2)O1O2=4-3=1时,两圆内切,t=(6-1)÷2=2.5秒,当O1O2=7时,两圆外切,t=(6+7)÷2=6.5秒;
当O1O2=4-3=1时,两圆内切,t=(原来的圆心距+现在的圆心距)÷2=(6+1)÷2=3.5秒;
(3)若C,B,D在同一直线上,则应有∠ABC=∠ABD=90°,此时AC,AD分别是圆的直径,∠CAD也是直角;由勾股定理知CD=10,O1O2是△ACD的CD边对的中位线,O1O2=5,t=(6-5)÷2=0.5秒,或者t=(6-5+5)÷2=3秒.
(2)O1O2=4-3=1时,两圆内切,t=(6-1)÷2=2.5秒,当O1O2=7时,两圆外切,t=(6+7)÷2=6.5秒;
当O1O2=4-3=1时,两圆内切,t=(原来的圆心距+现在的圆心距)÷2=(6+1)÷2=3.5秒;
(3)若C,B,D在同一直线上,则应有∠ABC=∠ABD=90°,此时AC,AD分别是圆的直径,∠CAD也是直角;由勾股定理知CD=10,O1O2是△ACD的CD边对的中位线,O1O2=5,t=(6-5)÷2=0.5秒,或者t=(6-5+5)÷2=3秒.
解答:(1)证明:∵CA是圆O2的切线,DA是圆O1的切线,
∴∠CAB=∠D,∠DAB=∠C,
∴△ABC∽△DBA,
∴AB:BD=BC:AB,
即AB2=BC•BD;
解:(2)当O1O2=4-3=1时,两圆内切,t=(原来的圆心距-现在的圆心距)÷2=(6-1)÷2=2.5秒,
当O1O2=7时,两圆外切,t=(原来的圆心距+现在的圆心距)÷2=(6+7)÷2=6.5秒;
当O1O2=4-3=1时,两圆内切,t=(原来的圆心距+现在的圆心距)÷2=(6+1)÷2=3.5秒;
(3)能,分两种情况:
①当AC是圆O1的直径,AD是圆O2的直径时,∠ABC=∠ABD=90°,
∵∠CAB=∠D,∠DAB=∠C,
∴∠CAD=∠CAB+∠DAB=180°÷2=90°,
∴由勾股定理得CD=10cm,
∵圆心是直径的中点,
∴O1O2=CD÷2=5,t=(6-5)÷2=0.5秒;
②当t=(6+5)÷2=5.5秒时,三点B,C,D在同一直线上.
∴∠CAB=∠D,∠DAB=∠C,
∴△ABC∽△DBA,
∴AB:BD=BC:AB,
即AB2=BC•BD;
解:(2)当O1O2=4-3=1时,两圆内切,t=(原来的圆心距-现在的圆心距)÷2=(6-1)÷2=2.5秒,
当O1O2=7时,两圆外切,t=(原来的圆心距+现在的圆心距)÷2=(6+7)÷2=6.5秒;
当O1O2=4-3=1时,两圆内切,t=(原来的圆心距+现在的圆心距)÷2=(6+1)÷2=3.5秒;
(3)能,分两种情况:
①当AC是圆O1的直径,AD是圆O2的直径时,∠ABC=∠ABD=90°,
∵∠CAB=∠D,∠DAB=∠C,
∴∠CAD=∠CAB+∠DAB=180°÷2=90°,
∴由勾股定理得CD=10cm,
∵圆心是直径的中点,
∴O1O2=CD÷2=5,t=(6-5)÷2=0.5秒;
②当t=(6+5)÷2=5.5秒时,三点B,C,D在同一直线上.
点评:本题利用了弦切角定理,两圆的位置关系,直径对的圆周角是直角,勾股定理,三角形的中位线的判定和性质求解,注意第2,3小题都有两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为( )
如图,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为( )| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
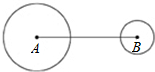 如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长( )
如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长( ) 如图,⊙A和⊙B内切,它们的半径分别为3和1,过A点作⊙B的切线,切点为C,则AC的长为( )
如图,⊙A和⊙B内切,它们的半径分别为3和1,过A点作⊙B的切线,切点为C,则AC的长为( ) 如图,⊙A、⊙B的半径分别为4、2,且AB=12,若做一⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,⊙C与⊙B相交于两点,则⊙C的半径可能是( )
如图,⊙A、⊙B的半径分别为4、2,且AB=12,若做一⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,⊙C与⊙B相交于两点,则⊙C的半径可能是( ) 和⊙
和⊙ 内切,它们的半径分别为3和1,过
内切,它们的半径分别为3和1,过 的切线,切点为
的切线,切点为 ,则
,则 的长为( )
的长为( )

