题目内容
 如图,⊙A和⊙B内切,它们的半径分别为3和1,过A点作⊙B的切线,切点为C,则AC的长为( )
如图,⊙A和⊙B内切,它们的半径分别为3和1,过A点作⊙B的切线,切点为C,则AC的长为( )分析:连接过切点的半径,构造直角三角形,根据两圆内切,得到两圆的圆心距,再根据勾股定理进行计算.
解答: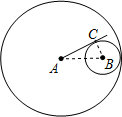 解:连接BC,
解:连接BC,
根据切线的性质,得∠ACB=90°,
根据两圆内切,得AB=3-1=2,
根据勾股定理,得AC=
=
.
故选:C.
 解:连接BC,
解:连接BC,根据切线的性质,得∠ACB=90°,
根据两圆内切,得AB=3-1=2,
根据勾股定理,得AC=
| 22-12 |
| 3 |
故选:C.
点评:此题主要考查了切线的性质、勾股定理以及根据两圆内切,正确计算两圆的圆心距是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为( )
如图,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为( )| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
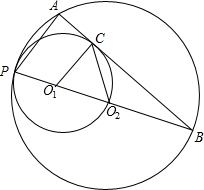 接AB,过O1作O1C⊥BA于C,连接CO2.已知PA=
接AB,过O1作O1C⊥BA于C,连接CO2.已知PA= 13、如图,⊙Ol和⊙O2内切于点P,⊙O2的弦AB经过⊙Ol的圆心Ol,交⊙Ol于C、D,若AC:CD:DB=3:4:2,则⊙Ol与⊙O2的直径之比为( )
13、如图,⊙Ol和⊙O2内切于点P,⊙O2的弦AB经过⊙Ol的圆心Ol,交⊙Ol于C、D,若AC:CD:DB=3:4:2,则⊙Ol与⊙O2的直径之比为( )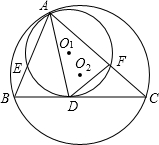 D平分∠BAC.
D平分∠BAC. (2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.
(2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.