题目内容
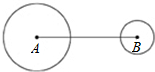 如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长( )
如图,圆A、圆B的半径分别为4、2,且AB=12.若作一圆C使得三圆的圆心在同一直在线,且圆C与圆A外切,圆C与圆B相交于两点,则下列何者可能是圆C的半径长( )| A、3 | B、4 | C、5 | D、6 |
分析:首先找到一个圆和圆A和圆B都外切,求出该圆的半径,然后再找到圆C和圆A外切和圆B相内切时,圆C半径的取值.
解答:解:当圆C和两圆都外切时,
根据题意我们可知圆C的半径r=3,
当圆C和圆A外切和圆B相内切时,
圆C的半径r=5,
故圆C与圆A外切,圆C与圆B相交于两点,
圆C的半径取值范围为3<r<5,
故选B.
根据题意我们可知圆C的半径r=3,
当圆C和圆A外切和圆B相内切时,
圆C的半径r=5,
故圆C与圆A外切,圆C与圆B相交于两点,
圆C的半径取值范围为3<r<5,
故选B.
点评:本题主要考查圆与圆的位置关系的知识点,解答本题的关键是根据圆心距和两圆半径之间的关系进行着手解答,本题比较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
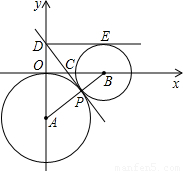
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,
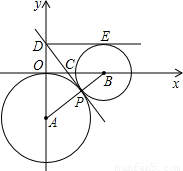
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,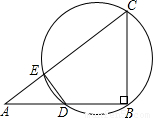
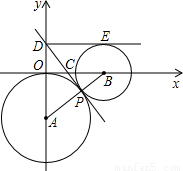
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,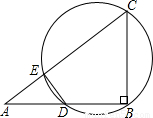
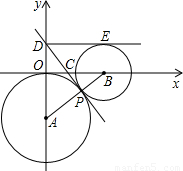
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,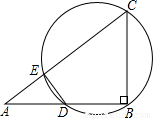
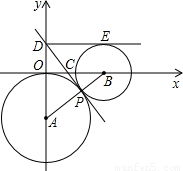
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,