题目内容
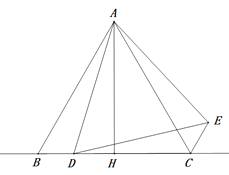
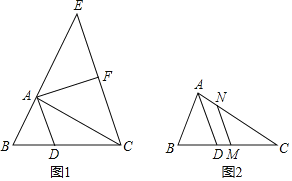
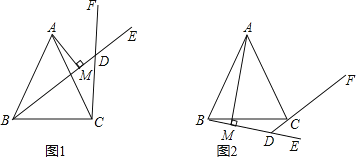
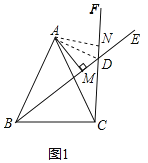
【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
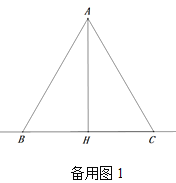
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
【答案】(1)∠BDC=∠CAB,见解析;(2)见解析;(3)不成立,BM=DM﹣DC,见解析
【解析】
(1)由三角形内角和定理得出![]() ,
,![]() ,又∠ABE=∠ACF,则进行计算即可得解;
,又∠ABE=∠ACF,则进行计算即可得解;
(2)作AN⊥CF于N,连接AD,易证![]() ,由AAS证得△AMB≌△ANC得出BM=CN=DC+DN,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论;
,由AAS证得△AMB≌△ANC得出BM=CN=DC+DN,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论;
(3)作AN⊥CF于N,连接AD,易证![]() ,由AAS证得△AMB≌△ANC得出
,由AAS证得△AMB≌△ANC得出![]() ,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论.
,AM=AN,由HL证得Rt△AMD≌Rt△AND得出DM=DN,即可得出结论.
(1)解:∠BDC=∠CAB;理由如下:
∵![]() ,
,
![]() ,
,
∠ABE=∠ACF,
∴![]()
=![]()
=![]()
∴![]() ;
;
(2)证明:作AN⊥CF于N,连接AD,如图1所示:
∵AM⊥BD,
∴![]() ,
,
在△AMB和△ANC中,
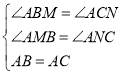 ,
,
∴△AMB≌△ANC![]() ,
,
∴BM=CN=DC+DN,AM=AN,
在Rt△AMD和Rt△AND中,
![]() ,
,
∴Rt△AMD≌Rt△AND![]() ,
,
∴DM=DN,
∴BM=DM+DC;
(3)不成立,BM=DM﹣DC;理由如下:
作AN⊥CF于N,连接AD,如图2所示:
∵AM⊥BD,
∴![]() ,
,
在△AMB和△ANC中,
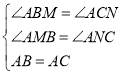 ,
,
∴△AMB≌△ANC![]() ,
,
∴![]() ,AM=AN,
,AM=AN,
在Rt△AMD与Rt△AND中,
![]() ,
,
∴Rt△AMD≌Rt△AND![]() ,
,
∴DM=DN,
∴![]() .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案