题目内容
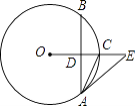
【题目】如图,一枚棋子放在⊙O上的点A处,通过摸球来确定该棋子的走法.
其规则如下:在一只不透明的口袋中,装有3个标号分别为1,2,3的相同小球.充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,若摸出的两个小球标号之积是m,就沿着圆周按逆时针方向走m步(例如:m=1,则A﹣B;若m=6,则A﹣B﹣C﹣D﹣A﹣B﹣C).用列表或树状图,分别求出棋子走到A、B、C、D点的概率.
【答案】解:画树状图得:
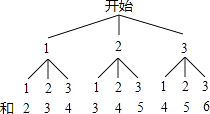
∵共有9种等可能的结果,棋子走到A点的有3种情况(点数和为4),棋子走到B点的有2种情况(点数和为5),棋子走到C点的有2种情况(点数和为2或6),棋子走到D点的有2种情况(点数和为3),
∴P(棋子走到A点)= ![]() =
= ![]() ,P(棋子走到B点)=P(棋子走到C点)=P(棋子走到D点)=
,P(棋子走到B点)=P(棋子走到C点)=P(棋子走到D点)= ![]() .
.
【解析】抓住题中关键的已知条件,充分搅匀后从中随机摸出1个,记下标号后放回袋中并搅匀,再从中随机摸出1个,画出树状图,求出所有可能的结果数,及分别求出棋子走到A点、棋子走到B点、棋子走到C点、棋子走到D的可能数,然后利用概率公式即可求出它们的概率。
【考点精析】本题主要考查了列表法与树状图法的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校兴趣小组,对函数y=|x﹣1|+1的图像和性质进行了研究,探究过程如下:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值如表:
的几组对应值如表:
X | …… |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | …… |
其中![]()
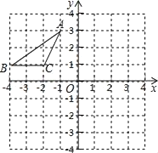
(2)在平面直角坐标系中,画出上表中对应值为点的坐标,根据画出的点,画出该函数的图象;

(3)根据画出的函数图像特征,仿照示例,完成下表中函数的变化规律:
序号 | 函数图像特征 | 函数变化规律 |
示例1 | 在直线 | 当 |
① | 在直线 |
|
示例2 | 函数图像经过点(-3,5) | 当 |
② | 函数图像的最低点是 | 当 |
(4)当![]() 时,
时,![]() 的取值范围是_____________
的取值范围是_____________