Question

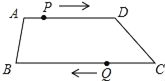
【题目】如图，在四边形ABCD中，AD∥BC，AD＝12cm，BC＝15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t（s）．

（1）用含t的代数式表示：

AP＝　 　；DP＝　 　；BQ＝　 　；CQ＝　 　．

（2）当t为何值时，四边形APQB是平行四边形？

（3）当t为何值时，四边形PDCQ是平行四边形？

Answer 1

【答案】（1）t，12﹣t，15﹣2t，2t（2）t＝5s时四边形APQB是平行四边形（3）当t＝4s时，四边形PDCQ是平行四边形

【解析】

（1）根据速度、路程以及时间的关系和线段之间的数量关系，即可求出AP，DP，BQ，CQ的长；

（2）当AP＝BQ时，四边形APQB是平行四边形，建立关于t的一元一次方程方程，解方程求出符合题意的t值即可；

（3）当PD＝CQ时，四边形PDCQ是平行四边形；建立关于t的一元一次方程方程，解方程求出符合题意的t值即可．

解：（1）AP=t，DP =12﹣t，BQ=15﹣2t，CQ=2t；

（2）根据题意有AP＝t，CQ＝2t，PD＝12﹣t，BQ＝15﹣2t．

∵AD∥BC，

∴当AP＝BQ时，四边形APQB是平行四边形，

∴t＝15﹣2t，解得t＝5，

∴t＝5s时四边形APQB是平行四边形；

（3）由AP＝tcm，CQ＝2tcm，

∵AD＝12cm，BC＝15cm，

∴PD＝AD﹣AP＝12﹣t，

如图1，∵AD∥BC，

∴当PD＝QC时，四边形PDCQ是平行四边形．

即：12﹣t＝2t，

解得t＝4s，

∴当t＝4s时，四边形PDCQ是平行四边形．