题目内容
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
(1)求证:∠ADC=∠ABD;
(2)若AD=2 ![]() ,⊙O的半径为3,求MD的长.
,⊙O的半径为3,求MD的长.
【答案】
(1)证明:连接OD,如图:
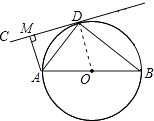
∵直线CD切⊙O于点D,∴∠CDO=90°,
∵AB为⊙O的直径,∴∠ADB=90°,
∴∠ADC+∠ADO=∠ADO+∠ODB=90°,∴∠ADC=∠ODB,
∵OB=OD,∴∠ODB=∠ADB,
∴∠ADC=∠ABD
(2)解:∵⊙O的半径为3,AB=6,
∵∠ADB=90°,∴DB═ ![]() ,
,
∵∠AMD=∠ADB=90°,∠ADC=∠ABD,
∴△ADM∽△ABD,
∴ ![]() ,即
,即 ![]()
∴DM=2 ![]()
【解析】(1)利用切线的性质定理,需连接OD,再利用直径所对圆周角是直角,可证出结论;(2)由(1)的结论结合垂直,可证出△ADM∽△ABD,对应边成比例可求出DM.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目