题目内容
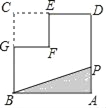
【题目】如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.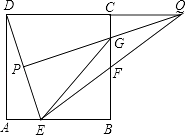
(1)求证:△ADE∽△PQD;
(2)求线段CQ的长;
(3)求∠EGB的正切值.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DC∥AB,
∴∠AED=∠PDQ,又∠DAE=∠QPD=90°,
∴△ADE∽△PQD
(2)解:由勾股定理得,DE= ![]() =
= ![]() ,
,
∵PQ是DE的垂直平分线,
∴DP= ![]() DE=
DE= ![]() ,
,
∵△ADE∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,DQ=5,
则CQ=DQ﹣DC=5﹣3=2
(3)解:由勾股定理得,PQ= ![]() =
= ![]() ,
,
∵∠QCG=∠QPD=90°,∠CQG=∠PQD,
∴△CQG∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CG= ![]() ,
,
∴BG=3﹣ ![]() =
= ![]() ,
,
∴tan∠EGB= ![]() =
= ![]()
【解析】(1)根据正方形的性质得到DC∥AB,得到∠AED=∠PDQ,根据两角对应相等的两个三角形相似证明;
(2)根据勾股定理求出DE,根据相似三角形的性质列出比例式,计算即可;
(3)根据相似三角形的性质求出CG,根据正切的概念计算即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目