Question

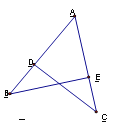
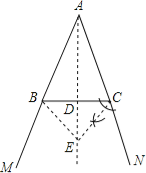
【题目】如图，点B和点C分别为∠MAN两边上的点，AB=AC.

（1）按下列语句画出图形：(要求不写作法，保留作图痕迹)

① AD⊥BC，垂足为D；

② ∠BCN的平分线CE与AD的延长线交于点E；

③ 连结BE.

（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形： ≌ ， ≌ ；并选择其中的一对全等三角形予以证明.

Answer 1

【答案】（1）作图见解析；（2）△ABE≌△ACE，△BDE≌△CDE．证明见解析.

【解析】试题分析：（1）①从A作AD⊥BC，垂足为D，D在线段BC上；

②作∠BCN的平分线CE与AD的延长线交于点E，E在线段AD的延长线上；

③连接BE就是过B、E两点画线段；

（2）还有△ABE≌△ACE；△BDE≌△CDE．其中证明△ABE≌△ACE的条件有AB=AC、∠BAE=∠CAE、AE公共，由此即可证明；证明△BDE≌△CDE的全等条件有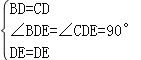，由此即可证明结论．

解：（1）①②③，如图所示：

（2）△ABE≌△ACE，△BDE≌△CDE．

（3）选择△ABE≌△ACE进行证明．

∵AB=AC，AD⊥BC，

∴∠BAE=∠CAE，

在△ABE和△ACE中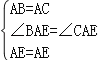

∴△ABE≌△ACE（SAS）；

选择△BDE≌△CDE进行证明．

∵AB=AC，AD⊥BC，

∴BD=CD，

在△BDE和△CDE中，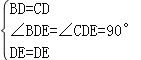

∴△BDE≌△CDE（SAS）．