题目内容
12、已知△ABC中，∠C是其最小的内角，过顶点B的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC与∠C之间的关系为
∠ABC=180°-3∠C或∠ABC=90°，∠C是小于45°的任意角．
．分析：设过B的直线交AC于D．因为没有指明是哪两个边相等，故应该分情况进行分析，从而求解．
解答：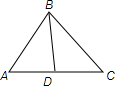
解：设过B的直线交AC于D．
∵BC≠BD（如果他们相等的话，则∠BAC比∠C还小，与题设矛盾），
∴BD=CD．
①若AB=BD，
∵AB=BD，
∴∠A=∠ADB=∠C+∠CBD=2∠C．
∵∠A+∠C+∠ABC=2∠C+∠C+∠ABC=180°，
∴∠ABC+3∠C=180°，
∴∠ABC=180°-3∠C．
②若BD=AD．
∵BD=AD，BD=CD，
∴DB=DC=DA，
∴∠ABC=90°，
∵∠C是最小的角，
∴∠C是小于45°的任意角．
故答案为：∠ABC=180°-3∠C或∠ABC=90°，∠C是小于45°的任意角．
解：设过B的直线交AC于D．∵BC≠BD（如果他们相等的话，则∠BAC比∠C还小，与题设矛盾），
∴BD=CD．
①若AB=BD，
∵AB=BD，
∴∠A=∠ADB=∠C+∠CBD=2∠C．
∵∠A+∠C+∠ABC=2∠C+∠C+∠ABC=180°，
∴∠ABC+3∠C=180°，
∴∠ABC=180°-3∠C．
②若BD=AD．
∵BD=AD，BD=CD，
∴DB=DC=DA，
∴∠ABC=90°，
∵∠C是最小的角，
∴∠C是小于45°的任意角．
故答案为：∠ABC=180°-3∠C或∠ABC=90°，∠C是小于45°的任意角．
点评：此题主要考查等腰三角形的性质，三角形外角的性质及三角形内角和定理的综合运用．
练习册系列答案
相关题目
情况；若不可能，请说明理由．
已知△ABC中，DE∥BC，EF∥AB，AB=3，BC=6，AD：DB=2：1，则四边形DBFE的周长为
如图所示，已知△ABC中，AB=AC，以AB为直径作⊙O交BC于D，交AC于E，过D作DF⊥AC于F
如图，已知△ABC中，AB=AC，AB垂直平分线交AC于D，连接BE，若∠A=40°，则∠EBC=（ ）