题目内容
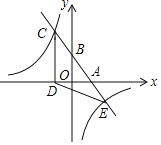
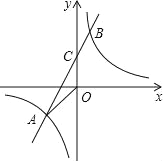
【题目】如图，已知A（n，﹣2），B（1，4）是一次函数y=kx+b的图象与反比例函数y=
的图象的两个交点，直线AB与y轴交于点C．
（1）求反比例函数和一次函数的解析式；
（2）求△AOC的面积．
【答案】（1）反比例函数解析式为y=
，一函数解析式为y=2x+2；（2）△AOC的面积是2.
【解析】
（1）根据A（n，﹣2），B（1，4）是一次函数y＝kx+b的图象与反比例函数y
的图象的两个交点，可以求得m的值，进而求得n的值，即可解答本题；
（2）根据函数图象和（1）中一次函数的解析式可以求得点C的坐标，从而可以求得△AOC的面积．
（1）∵A（n，﹣2），B（1，4）是一次函数y＝kx+b的图象与反比例函数y的图象的两个交点，∴4
，得：m＝4，∴y
，∴﹣2
，得：n＝﹣2，∴点A（﹣2，﹣2），∴
，得：
，∴一次函数解析式为y＝2x+2，即反比例函数解析式为y，一次函数解析式为y＝2x+2；
（2）当x＝0时，y＝2×0+2＝2，∴点C的坐标是（0，2）．
∵点A（﹣2，﹣2），点C（0，2），∴△AOC的面积是：
．
练习册系列答案
相关题目
【题目】2020年东京奥运会的比赛门票开始接受公众预订．下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格，球迷小李用12000元做为预订下表中比赛项目门票的资金．
比赛项目 | 票价(元／场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票共15张，问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下，这个球迷想预定上表中三种球类门票，其中足球门票与乒乓球门票数相同，且足球门票的费用不超过男篮门票的费用，问可以预订这三种球类门票各多少张？
