Question

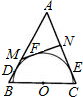如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E．过半圆上一点F作半圆的切线，分别交AB，AC于M，N．那么

BM•CN

BC2

的值等于（　　）

• A、

  1

  8

• B、

  1

  4

• C、

  1

  2

• D、1

Answer 1

分析：连OM，ON，利用切线长定理知OM，ON分别平分角BMN，角CNM，再利用三角形和四边形的内角和可求得△OBM与△NOC还有一组角相等，由此得到它们相似，通过相似比可解决问题．

解答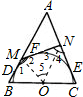：解：连OM，ON，如图
∵MD，MF与⊙O相切，
∴∠1=∠2，
同理得∠3=∠4，
而∠1+∠2+∠3+∠4+∠B+∠C=360°，AB=AC
∴∠2+∠3+∠B=180°；
而∠1+∠MOB+∠B=180°，
∴∠3=∠MOB，即有∠4=∠MOB，
∴△OMB∽△NOC，
∴

BM

OC

=

OB

CN

，
∴BM•CN=

1

4

BC²，
∴

BM•CN

BC2

=

1

4

．
故选B．

点评：熟练掌握三角形相似的判定；熟悉切线长定理；记住三角形和四边形的内角和．另外对于此类题型要找到含有比中的线段的三角形，证明它们相似，有的要先进行线段的等量代换．