��Ŀ����
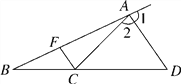
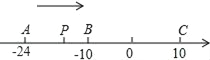
����Ŀ����ͼ��ֱ��x��ֱ��y��ֱ�ڵ�O����B��C��ֱ��x�ϣ���A��ֱ��x�⣬����AC��AB�õ���ABC.
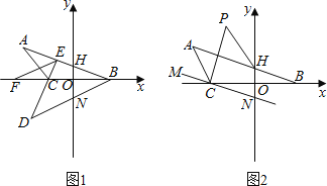
��1������ABC��ֱ��x�۵���ʹ��A���ڵ�D�����ӳ�DC��AB�ڵ�E��EFƽ����AED��ֱ��x�ڵ�F.
������EFB=25������DEF=10��������DCF=______
������ACF-��AEF=18��������EFB�Ķ�����
��2������C��MNƽ����AB��ֱ��y�ڵ�N��CPƽ����BCM��HPƽ����AHY������C�ӵ�O��ֱ��x�����˶�ʱ����CPH�Ķ����Ƿ����仯��������������������仯������仯��Χ.
���𰸡�(1)��35������18����(2)���䣮
��������
��1������������������ʿɵã�
�����۵������ʿɵá�A=��D����ABC=��DBC���ɽ�ƽ���ߵ����ʿɵá�AEF=��FED=![]() ��AED=
��AED=![]() ��A+��ABC���������ε�������ʿ����EFB�Ķ�����
��A+��ABC���������ε�������ʿ����EFB�Ķ�����
��2����ƽ���ߵ����ʿɵá�PGA=��PCM����AHY=��CNO���ɽ�ƽ���ߵ����ʿɵá�PCM=![]() ��BCM=��PGA����PHG=
��BCM=��PGA����PHG=![]() ��AHY=
��AHY=![]() ��CNO���������ε���ǵ����ʿ����CPH=45����
��CNO���������ε���ǵ����ʿ����CPH=45����
�⣺��1���١ߡ�DCF=��EFB+��DEF=25��+10��
���DCF=35��
�ʴ�Ϊ35��
�ڡ߽���ABC��ֱ��x�۵���ʹ��A���ڵ�D����
���A=��D����ABC=��DBC
�ߡ�AED=��D+��EBD
���AED=��A+2��ABC
��EFƽ�֡�AED
���AEF=��FED=![]() ��AED=
��AED=![]() ��A+��ABC
��A+��ABC
�ߡ�AEF=��EFB+��ABC
���EFB=![]() ��A
��A
�ߡ�ACF=��A+��ABC���ҡ�ACF-��AEF=18����
���A+��ABC-��![]() ��A+��ABC��=18��
��A+��ABC��=18��
���A=36��
���EFB=![]() ��A=18��
��A=18��
��2������
��ͼ��
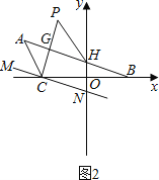
��AB��MN
���PGA=��PCM����AHY=��CNO
��CPƽ�֡�BCM��HPƽ�֡�AHY
���PCM=![]() ��BCM=��PGA����PHG=
��BCM=��PGA����PHG=![]() ��AHY=
��AHY=![]() ��CNO
��CNO
�ߡ�BCM=��CNO+��CON
��![]() ��BCM=
��BCM=![]() ��CNO+45��
��CNO+45��
���PGA=��PHG+45��
�ߡ�PGA=��GPH+��PHG
���CPH=45��

����Ŀ��ijУΪ���˽�ѧ�������ġ���ѧ��Ӣ������ĿƵ�ϲ���̶ȣ�ÿ��ֻѡһ�ƣ����ض��꼶ij������˵��飬�����Ƴ�����Ƶ����Ƶ��ͳ�Ʊ�������ͳ��ͼ��
��Ŀ | Ƶ�� | Ƶ�� |
���� |
| 0.5 |
��ѧ | 12 |
|
Ӣ�� | 6 |
|
���� |
| 0.2 |

��1������������������
��2���������![]() ��ֵ��
��ֵ��
��3������У���꼶��ѧ��1000�ˣ��������ϲ��Ӣ�����������������Ŀ���.
����Ŀ��ij�����̴��г���֪������Ϣ��
ijƷ�ƿյ��� | ijƷ�Ƶ���� | |
���ۣ�Ԫ/̨�� | 700 | 100 |
�ۼۣ�Ԫ/̨�� | 900 | 160 |
������40000Ԫ�ʽ������һ���Թ�����Ʒ�ƿյ��Ⱥ͵���ȹ�100̨����þ����̹����յ���![]() ̨���յ��Ⱥ͵����ȫ���������������Ϊ
̨���յ��Ⱥ͵����ȫ���������������Ϊ![]() Ԫ.
Ԫ.
��1����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2�����ú������ʣ�˵���þ�������ν����ɻ��������������Ƕ���Ԫ��