题目内容
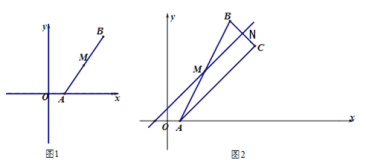
【题目】(1)如图1中,△ABC为正三角形,点E为AB边上任一点,以CE为边作正△DEC,连结AD.求![]() 的值.
的值.
(2)如图2中,△ABC为等腰直角三角形,∠A=90°,点E为腰AB上任意一点,以CE为斜边作等腰直角△CDE,连结AD.求![]() 的值;
的值;
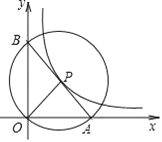
(3)如图3中,△ABC为任意等腰三角形,点E为腰AB上任意一点,以CE为底边作等腰△DEC,使△DEC∽△ABC,并且BC=![]() AC.连结AD,直接写出
AC.连结AD,直接写出![]() 的值.
的值.

【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由三角形ABC与三角形CDE都为正三角形,得到AB=AC,CE=CD,以及内角为60°,利用等式的性质得到∠ECB=∠DCA,利用SAS得到三角形ECB与三角形DCA全等,利用全等三角形对应边相等得到BE=AD,即可求出所求之比;
(2)由三角形CDE与三角形ABC都为等腰直角三角形,利用等腰直角三角形的性质得到CE=![]() CD,BC=
CD,BC=![]() AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
(3)仿照前两问,以此类推得到一般性规律,求出所求之比即可.
解:(1)∵△ABC和△CDE都是正三角形,
∴∠B=∠ACB=∠DCE=60°,AB=AC,CE=DC,
∵∠ECB=∠ACB﹣∠ACE=60°﹣∠ACE,
∠DCA=∠DCE﹣∠ACE=60°﹣∠ACE,
∴∠ECB=∠DCA,
在△ECB和△DCA中,
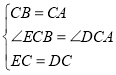 ,
,
∴△ECB≌△DCA(SAS),
∴BE=AD,
则![]() =1;
=1;
(2)∵等腰Rt△ABC和等腰Rt△CDE中,
∴∠B=∠ACB=∠DCE=45°,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB﹣∠ACE=45°﹣∠ACE,
∠ACD=∠DCE﹣∠ACE=45°﹣∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴![]() ;
;
(3)依此类推,当BC=![]() AC时,
AC时,![]() =
=![]() ,理由为:
,理由为:
∵等腰△ABC和等腰△CDE中,
∴∠B=∠ACB=∠DCE,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB﹣∠ACE,∠ACD=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴![]() =
=![]() .
.