Question

【题目】在平面直角坐标系xOy（如图）中，抛物线y＝ax2+bx+2经过点A（4，0）、B（2，2），与y轴的交点为C．

（1）试求这个抛物线的表达式；

（2）如果这个抛物线的顶点为M，求△AMC的面积；

（3）如果这个抛物线的对称轴与直线BC交于点D，点E在线段AB上，且∠DOE＝45°，求点E的坐标．

Answer 1

【答案】（1）y＝；（2）；（3）点E的坐标为（3，1）．

【解析】

（1）根据点A，B的坐标，利用待定系数法即可求出抛物线的表达式；

（2）利用配方法可求出点M的坐标，利用二次函数图象上点的坐标特征可求出点C的坐标，过点M作MH⊥y轴，垂足为点H，利用分割图形求面积法可得出△AMC的面积；

（3）连接OB，过点B作BG⊥x轴，垂足为点G，则△BGA，△OCB是等腰直角三角形，进而可得出∠BAO＝∠DBO，由∠DOB＋∠BOE＝45°，∠BOE＋∠EOA＝45°可得出∠EOA＝∠DOB，进而可证出△AOE∽△BOD，利用相似三角形的性质结合抛物线的对称轴为直线x＝1可求出AE的长，过点E作EF⊥x轴，垂足为点F，则△AEF为等腰直角三角形，根据等腰直角三角形的性质可得出AF、EF的长，进而可得出点E的坐标．

解：（1）将A（4，0），B（2，2）代入y＝ax2＋bx＋2，得：，

解得：，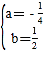

∴抛物线的表达式为y＝﹣x2＋x＋2．

（2）∵y＝﹣x2＋x＋2＝﹣（x﹣1）2＋，

∴顶点M的坐标为（1，）．

当x＝0时，y＝﹣x2＋x＋2＝2，

∴点C的坐标为（0，2）．

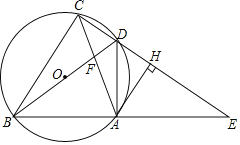
过点M作MH⊥y轴，垂足为点H，如图1所示．

∴S△AMC＝S梯形AOHM﹣S△AOC﹣S△CHM，

＝（HM＋AO）OH﹣AOOC﹣CHMH，

＝×（1＋4）×﹣×4×2﹣×（﹣2）×1，

＝．

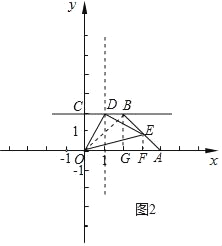
（3）连接OB，过点B作BG⊥x轴，垂足为点G，如图2所示．

∵点B的坐标为（2，2），点A的坐标为（4，0），

∴BG＝2，GA＝2，

∴△BGA是等腰直角三角形，

∴∠BAO＝45°．

同理，可得：∠BOA＝45°．

∵点C的坐标为（2，0），

∴BC＝2，OC＝2，

∴△OCB是等腰直角三角形，

∴∠DBO＝45°，BO＝2，

∴∠BAO＝∠DBO．

∵∠DOE＝45°，

∴∠DOB＋∠BOE＝45°．

∵∠BOE＋∠EOA＝45°，

∴∠EOA＝∠DOB，

∴△AOE∽△BOD，

∴．

∵抛物线y＝﹣x2＋x＋2的对称轴是直线x＝1，

∴点D的坐标为（1，2），

∴BD＝1，

∴，

∴AE＝，

过点E作EF⊥x轴，垂足为点F，则△AEF为等腰直角三角形，

∴EF＝AF＝1，

∴点E的坐标为（3，1）．