题目内容
【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是 ．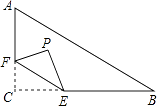 
【答案】1.2
【解析】解：如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．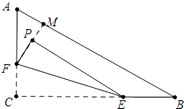 
∵∠A=∠A，∠AMF=∠C=90°，
∴△AFM∽△ABC，
∴ 
= 
，
∵CF=2，AC=6，BC=8，
∴AF=4，AB= 
=10，
∴ 
= 
，
∴FM=3.2，
∵PF=CF=2，
∴PM=1.2
∴点P到边AB距离的最小值是1.2．
故答案为1.2．
如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小，利用△AFM∽△ABC，得到 = 求出FM即可解决问题．
练习册系列答案
相关题目
【题目】某工厂分发年终奖金，具体金额和人数如下表所示，则下列对这组数据的说法中不正确的是（ ）
人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
金额（元） | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
A.极差是195000
B.中位数是15000
C.众数是15000
D.平均数是15000
