题目内容
已知:在四边形ABCD中,AC = BD,AC与BD交于点O,∠DOC = 60°.
小题1:当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
小题2:当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
小题3:如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
小题1:当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
小题2:当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
小题3:如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.

小题1:在?ABCD中,∵AC=BD
∴?ABCD为矩形
又∵∠DOC=60°,
∴∠AOB=60°,
又OA=OB=OC=OD,
∴AB=CD=OA=OC.
即AB+CD=AC;(3分)
小题2:AB+CD=AC;
∵∠DOC=60°,
∴∠AOB=60°,
∵AC=BD,
∴△AOB,△DOC都是正三角形,
∴OA=OB=AB,OD=OC=DC
即AB+CD=AO+C0=AC;(3分)
小题3:不成立,应为AB+CD>AC.
如图所示过B作BM∥AC,过C作CM∥AB,
则四边形ABMC为平行四边形,
∴CM=AB,BM=AC=BD,BM∥AC,
又∵∠DOC=60°,
∴∠DBM=∠DOC=60°
即三角形DBM为等边三角形,
∴BM=AC=DM
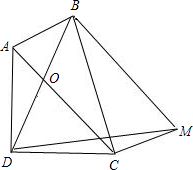
在△CDM中,CM+CD>DM,
即AB+CD>AC.(4分)
(1)当四边形ABCD为平行四边形时,由于AC=BD,所以平行四边形ABCD实际为矩形,若∠DOC=60°时,三角形ABO和三角形DOC均为等边三角形,所以会有AB+CD=AC;
(2)当四边形ABCD为等腰梯形时,三角形ABO和三角形CDO也是等边三角形,所以会有AB+CD=AC;
(3)不成立,过B作BM∥AC,过C作CM∥AB,连接DM.构建平行四边形后AB=CM,BM=AC=BD,由于∠DOC=60°,可知∠DBM=60°,即三角形BDM为等边三角形,所以BD=BM=DM=AC,在三角形DCM中,CM+CD>AC,即AB+CD>AC.
(2)当四边形ABCD为等腰梯形时,三角形ABO和三角形CDO也是等边三角形,所以会有AB+CD=AC;
(3)不成立,过B作BM∥AC,过C作CM∥AB,连接DM.构建平行四边形后AB=CM,BM=AC=BD,由于∠DOC=60°,可知∠DBM=60°,即三角形BDM为等边三角形,所以BD=BM=DM=AC,在三角形DCM中,CM+CD>AC,即AB+CD>AC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 C.
C. D.
D.





 沿直线
沿直线 折叠,顶点
折叠,顶点 恰好落在
恰好落在 边上
边上 点处,已知
点处,已知 ,
, ,则图中阴影部分面积为 __.
,则图中阴影部分面积为 __.
