题目内容
【题目】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=62°,∠ACB=29°,求∠FGC的度数.

【答案】(1)见解析;(2)85°.
【解析】
(1)由旋转的性质可得AC=AF,利用SAS证明△ABC≌△AEF,根据全等三角形的对应边相等即可得出EF=BC;
(2)根据等腰三角形的性质以及三角形内角和定理求出∠BAE=180°-62°×2=56°,那么∠FAG=56°.由△ABC≌△AEF,得出∠F=∠ACB=29°,再根据三角形外角的性质即可求出∠FGC=∠FAG+∠F=85°.
(1)证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF.
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF.
在△ABC与△AEF中,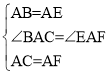 ,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
(2)解:∵AB=AE,∠ABC=62°,
∴∠BAE=180°-62°×2=56°,
∴∠CAF=∠BAE =56°.
∵△ABC≌△AEF,
∴∠F=∠ACB=29°,
∴∠FGC=∠CAF+∠F=56°+29°=85°.

练习册系列答案
相关题目




