题目内容
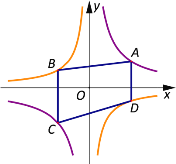
【题目】如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.
上,AD// BC//y 轴.
(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;
(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;
(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.

【答案】(I) 点![]() 的坐标为
的坐标为![]() ;(II) 四边形
;(II) 四边形![]() 是平行四边形,理由见解析;(III)
是平行四边形,理由见解析;(III) ![]() 的最小值是
的最小值是![]() .
.
【解析】
(I)由![]() ,
,![]() ,可得
,可得![]() ,
,![]() .分别表示出点A、D的坐标,根据
.分别表示出点A、D的坐标,根据![]() ,即可求出点A的坐标.
,即可求出点A的坐标.
(II)根据点A、C关于原点O对称,设点A的坐标为:![]() ,即可分别表示出B、C、D的坐标,然后可得出
,即可分别表示出B、C、D的坐标,然后可得出![]() 与
与![]() 互相平分可证明出四边形
互相平分可证明出四边形![]() 是平行四边形.
是平行四边形.
(III) 设![]() 与
与![]() 的距离为
的距离为![]() ,由
,由![]() ,
,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,可求出h=7,根据
,可求出h=7,根据![]() ,
,![]() ,可得
,可得![]() ,进而得出答案.
,进而得出答案.
(I) ∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
由![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴此时点![]() 的坐标为
的坐标为![]() .
.
(II)四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
设点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 、
、![]() 关于原点
关于原点![]() 对称,∴点
对称,∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ∥
∥![]() ∥
∥![]() 轴,且点
轴,且点![]() 、
、![]() 在双曲线
在双曲线![]() 上,
上,![]()
![]() ,
,
∴点![]()
![]() ,点
,点![]()
![]() ,
,
∴点B与点D关于原点O对称,即![]() ,且
,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
又点![]() 、C关于原点O对称,即
、C关于原点O对称,即![]() ,且
,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
∴![]() 与
与![]() 互相平分.
互相平分.
∴四边形![]() 是平行四边形.
是平行四边形.
(III)设![]() 与
与![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,![]() ,可得:
,可得: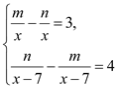 ,
,
则![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,
∴当![]() 取到等号 .
取到等号 .
即![]() ,
,![]() 时,
时, ![]() 的最小值是
的最小值是![]() .
.

【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]() ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?