题目内容
如图,在直角坐标系中,以AB为直径的⊙C交x轴于A,交y轴于B,满足OA:OB=4:3,以OC 为直径作⊙D,设⊙D的半径为2.
为直径作⊙D,设⊙D的半径为2.
(1)求⊙C的圆心坐标;
(2)过C作⊙D的切线EF交x轴于E,交y轴于F,求直线EF的解析式;
(3)抛物线y=ax2+bx+c(a≠0)的对称轴过C点,顶点在⊙C上,与y轴交点为B,求抛物线的解析式.
解:(1)∵OA⊥OB,OA:OB=4:3,⊙D的半径为2
∴⊙C过原点,OC=4,AB=8
A点坐标为( ,0)B点坐标为(0,
,0)B点坐标为(0, )
)
∴⊙C的圆心C的坐标为(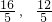 )
)
(2)由EF是⊙D的切线,
∴OC⊥EF
∵CO=CA=CB
∴∠COA=∠CAO,∠COB=∠CBO
∴Rt△AOB∽Rt△OCE∽Rt△FCO
∴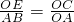 ,
,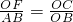
∴OE=5,OF=
∴E点坐标为(5,0),F点坐标(0, )
)
∴切线EF的解析式为y=- x+
x+ ;
;
(3)①当抛物线开口向下时,由题意,得
抛物线顶点坐标为( ,
, +4),
+4),
可得:- =
= ,
, =
= ,c=
,c=
∴a=- ,b=1,c=
,b=1,c= ,
,
∴y=- x2+x+
x2+x+ ;
;
②当抛物线开口向上时,
顶点坐标为( ,
, -4),
-4),
可得:- =
= ,
, =-
=- ,c=
,c= ,
,
∴y= x2-4x+
x2-4x+ ;
;
综上所述,抛物线解析式为:
y=- x2+x+
x2+x+ 或y=
或y= x2-4x+
x2-4x+ .
.
注:其他解法参照以上评分标准评分
分析:(1)⊙C以AB为直径,则C为Rt△OAB中斜边AB的中点,易知OC=4,那么AB=2OC=8;由OA、OB的比例关系,易知∠BAO的正切值,通过解直角三角形即可求得OB、OA的长,进而可求出A、B的坐标,也就能得到C点的坐标(若过C分别作OA、OB的垂线,由垂径定理即可求得C点的坐标);
(2)由(1)知OC是Rt△OAB斜边AB的中线,则BC=OC=AC,可得到∠BOC=∠CBO,∠COA=∠CAO;由此可证得Rt△AOB、Rt△OCE、Rt△FCO都相似,根据OC的长和相似三角形的比例线段即可求得OE、OF的长,也就得到了E、F的坐标,进而可用待定系数法求出直线EF的解析式;
(3)抛物线的对称轴过C点,且顶点在⊙C上,根据⊙C的半径及C点坐标,易求得抛物线的顶点坐标,又已知了B点的坐标,即可用待定系数法求出抛物线的解析式.(注意要分两种情况:①抛物线开口向上,②抛物线开口向下)
点评:此题综合考查了圆周角定理、相似三角形的判定和性质、一次函数及二次函数解析式的确定等知识,综合性强,难度较大.
∴⊙C过原点,OC=4,AB=8
A点坐标为(
 ,0)B点坐标为(0,
,0)B点坐标为(0, )
)∴⊙C的圆心C的坐标为(
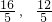 )
)(2)由EF是⊙D的切线,
∴OC⊥EF
∵CO=CA=CB
∴∠COA=∠CAO,∠COB=∠CBO
∴Rt△AOB∽Rt△OCE∽Rt△FCO
∴
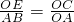 ,
,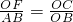
∴OE=5,OF=

∴E点坐标为(5,0),F点坐标(0,
 )
)∴切线EF的解析式为y=-
 x+
x+ ;
;(3)①当抛物线开口向下时,由题意,得
抛物线顶点坐标为(
 ,
, +4),
+4),可得:-
 =
= ,
, =
= ,c=
,c=
∴a=-
 ,b=1,c=
,b=1,c= ,
,∴y=-
 x2+x+
x2+x+ ;
;②当抛物线开口向上时,
顶点坐标为(
 ,
, -4),
-4),可得:-
 =
= ,
, =-
=- ,c=
,c= ,
,∴y=
 x2-4x+
x2-4x+ ;
;综上所述,抛物线解析式为:
y=-
 x2+x+
x2+x+ 或y=
或y= x2-4x+
x2-4x+ .
.注:其他解法参照以上评分标准评分
分析:(1)⊙C以AB为直径,则C为Rt△OAB中斜边AB的中点,易知OC=4,那么AB=2OC=8;由OA、OB的比例关系,易知∠BAO的正切值,通过解直角三角形即可求得OB、OA的长,进而可求出A、B的坐标,也就能得到C点的坐标(若过C分别作OA、OB的垂线,由垂径定理即可求得C点的坐标);
(2)由(1)知OC是Rt△OAB斜边AB的中线,则BC=OC=AC,可得到∠BOC=∠CBO,∠COA=∠CAO;由此可证得Rt△AOB、Rt△OCE、Rt△FCO都相似,根据OC的长和相似三角形的比例线段即可求得OE、OF的长,也就得到了E、F的坐标,进而可用待定系数法求出直线EF的解析式;
(3)抛物线的对称轴过C点,且顶点在⊙C上,根据⊙C的半径及C点坐标,易求得抛物线的顶点坐标,又已知了B点的坐标,即可用待定系数法求出抛物线的解析式.(注意要分两种情况:①抛物线开口向上,②抛物线开口向下)
点评:此题综合考查了圆周角定理、相似三角形的判定和性质、一次函数及二次函数解析式的确定等知识,综合性强,难度较大.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: