题目内容
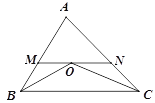
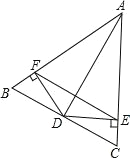
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是 ![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP. 
(1)求证:AB是⊙O的切线.
(2)若OA=4,则 ①当 ![]() 长为时,四边形OECF是菱形;
长为时,四边形OECF是菱形;
②当 ![]() 长为时,四边形OCBP是正方形.
长为时,四边形OCBP是正方形.
【答案】
(1)解:∵在△ABO中,OA=OB,C是AB的中点,
∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
(2)![]() ;
;![]()
【解析】(2)①∵OECF为菱形, ∴OE=EC,∠EOC=∠COF.
∴OE=EC=OC.
∴∠EOC=∠COF=60°.
∴∠DOF=60°.
又∵P为弧DF的中点,
∴∠DOP=30°.
∵∠AOC=60°,∠OCA=90°,
∴OC= ![]() OA=2.
OA=2.
∴弧DP的长= ![]() =
= ![]() .
.
②∵四边形OCBP为正方形,
∴∠COB=∠POB=45°.
∴OC= ![]() OB=2
OB=2 ![]() .
.
∵P为弧DF的中点,
∴∠DOP=45°.
∴弧DP的长= ![]() =
= ![]() .
.
所以答案是:① ![]() ;②
;② ![]() .
.
(1)由等腰三角形三线合一的性质可知OC⊥AB,依据题意可知OC为⊙O的半径,故此可证明AB是⊙O的切线;(2)①由菱形的性质可知:OE=EC,∠EOC=∠COF,然后证明△OEC为等边三角形可得到∠EOC的度数,然后可求得∠DOP的度数,接下来,在△OAC中,利用特殊锐角三角函数值可求得OC的长,最后依据弧长公式求解即可;②依据正方形的性质可求得OC= ![]() ,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
【考点精析】本题主要考查了等腰三角形的性质和正方形的判定方法的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案【题目】某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= , n= .
(2)若该市人口约有100万人,请你计算其中持D组“观点”的市民人数是多少万人?
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?