Question

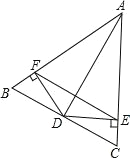
【题目】如图，三角形 ABC 中，∠A 的平分线交 BC 于点 D，过点 D 作 DE⊥AC， DF⊥AB，垂足分别为 E，F，下面四个结论：

①∠AFE＝∠AEF；②AD 垂直平分 EF；③；④EF 一定平行 BC． 其中正确的是（ ）

A. ①②③ B. ②③④ C. ①③④ D. ①②③④

Answer 1

【答案】A

【解析】

根据三角形全等的判定,中垂线概念即可,见详解.

解：①在△ABC中,AD是∠A的角平分线,DE⊥AC,DF⊥AB,

∵在△AFD和△AED中,

∠FAD=∠EAD, ∠AFD=∠AED,AD=AD

∴△AFD≌△AED（AAS）,

∴AF=AE,即△AEF为等腰三角形,

∴∠AFE=∠AEF.故①项正确.

②∵AF=AE,DF=DE,

∴A,D都在EF的垂直平分线上,

∴AD垂直平分EF.故②项正确.

③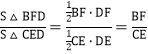,故③正确,

④∵AD不一定垂直BC,

∴EF不一定平行BC．故④错误.

综上①②③正确,故选A.