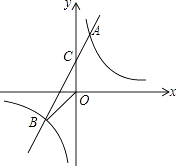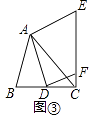��Ŀ����
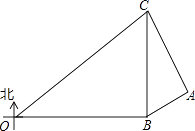
����Ŀ����ͼ��1������֪������y=ax2+bx��3�ĶԳ���Ϊx=1����x��ֱ���A��B���㣬��y�ύ�ڵ�C��һ�κ���y=x+1����A������y�ύ�ڵ�D��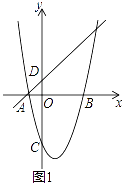
��1����������ߵĽ���ʽ��
��2����ͼ��2������PΪ������B��C����䲿���ϵ�����һ�㣨����B��C���㣩�����P�ĺ�����Ϊt�����ı���DCPB�����ΪS�����S��t�ĺ�����ϵʽ����ȷ��tΪ��ֵʱ��Sȡ���ֵ�����ֵ�Ƕ��٣�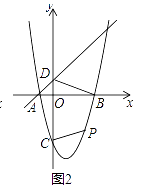
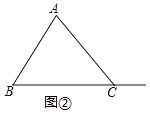
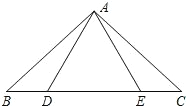
��3����ͼ��3��������ODB��ֱ��y=x+1ƽ�Ƶõ���O��D��B�䣬��O��B���������߽��ڵ�E������ED�䣬��ED��ǡ�ý���O��D��B��������Ϊ1��2�����֣���ֱ��д����ʱƽ�Ƶľ��룮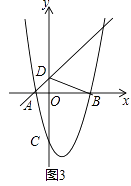
���𰸡�
��1��
�⣺��y=0����ֱ�ߵĽ���ʽ�ã�x+1=0�����x=��1��
��A����1��0����
�������ߵĶԳ���Ϊx=1��
��B��������3��0����
��x=0���������ߵĽ���ʽ�ã�y=��3��
��C��0����3����
�������ߵĽ���ʽΪy=a��x+1����x��3������C��0����3������ã���3a=��3�����a=1��
�������ߵĽ���ʽΪy=x2��2x��3��
��2��
�⣺��ͼ1��ʾ������OP��
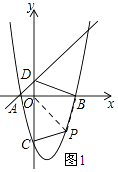
��x=0����ֱ��AD�Ľ���ʽ�ã�y=1��
��OD=1��
�������֪P��t��t2��2t��3����
���ı���DCPB�����=��ODB�����+��OBP�����+��OCP�������
��S= ![]() ��3��1+
��3��1+ ![]() ��3������t2+2t+3��+
��3������t2+2t+3��+ ![]() ��3��t�������ã�S=��
��3��t�������ã�S=�� ![]() t2+
t2+ ![]() t+6��
t+6��
�䷽�ã�S=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
�൱t= ![]() ʱ��Sȡ�����ֵ�����ֵΪ
ʱ��Sȡ�����ֵ�����ֵΪ ![]() ��
��
��3��
�⣺��ͼ2��ʾ��
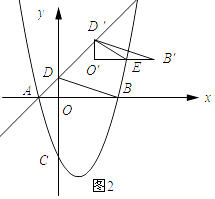
���D�������Ϊ��a��a+1����O�䣨a��a����
����D��O��E�������D��EB������=1��2ʱ����O��E��EB��=1��2��
��O��B��=0B=3��
��O��E=1��
��E��a+1��a����
����E��������������ߵĽ���ʽ�ã���a+1��2��2��a+1����3=a�������ã�a2��a��4=0����ã�a= ![]() ��a=
��a= ![]() ��
��
��O��������� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ����
����
��OO��= ![]() ��OO��=
��OO��= ![]() ��
��
���DOBƽ�Ƶľ���Ϊ ![]() ��
�� ![]() ��
��
����D��O��E�������D��EB������=2��1ʱ����O��E��EB��=2��1��
��O��B��=0B=3��
��O��E=2��
��E��a+2��a����
����E��������������ߵĽ���ʽ�ã���a+2��2��2��a+2����3=a�������ã�a2��a��4=0����ã�a= ![]() ��a=
��a= ![]() ��
��
��O��������� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ����
����
��OO��= ![]() ��OO��=
��OO��= ![]() ��
��
���DOBƽ�Ƶľ���Ϊ ![]() ��
�� ![]() ��
��
��������������D��O��B����DA����ƽ�� ![]() ��
�� ![]() ��λ���ȣ�����AD����ƽ��
��λ���ȣ�����AD����ƽ�� ![]() ��
�� ![]() ����λ����ʱ��ED��ǡ�ý���O��D��B��������Ϊ1��2�����֣�
����λ����ʱ��ED��ǡ�ý���O��D��B��������Ϊ1��2�����֣�
����������1������õ�A�����꣬Ȼ�����������ߵĶԳ��Կ���õ�B�����꣬Ȼ����õ�C�����꣬�������ߵĽ���ʽΪy=a��x+1����x��3������C��0����3���������a��ֵ���ɣ���2������OP������õ�D�����꣬�Ӷ��ɵõ�OD�ij�����P��t��t2��2t��3����Ȼ�������ı���DCPB�����=��ODB�����+��OBP�����+��OCP������ɵõ�S��t�ĺ�����ϵʽ�������䷽�������S�����ֵ�Լ���Ӧ��t��ֵ����3�����D�������Ϊ��a��a+1����O�䣨a��a��������D��O��E�������D��EB������=1��2ʱ��E��a+1��a��������E��������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ�O������꣬Ȼ�����OO��ij����ɣ�����D��O��E�������D��EB������=2��1ʱ��E��a+2��a����ͬ�������OO��ij����Ӷ��ɵõ���B��O��D��ƽ�Ƶľ��룮