题目内容
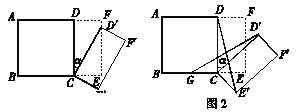
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
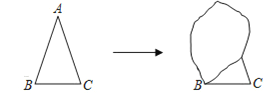
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

【答案】(1)能,具体见解析;(2)证明见解析.
【解析】
(1)方法1:量出 ∠C的大小;作∠B =∠C;则∠B的一条边和∠C的一条边的延长线交于点A;方法2:作边BC的垂直平分线与∠C的另一边的延长线交于点A,连接AB即可;方法3:将长方形纸片对折使点B和点C重合,找到∠ C的另一边的延长线与折痕的交点A,连接AB即可;
(2)证法1:作∠A的平分线AD,交BC与点D,利用AAS即可证出△ABD≌△ACD,从而得出AB=AC,根据等腰三角形的定义即可得出结论;证法2:过A作AD⊥BC于D,利用AAS即可证出△ABD≌△ACD,从而得出AB=AC,根据等腰三角形的定义即可得出结论.
解:(1)方法1:量出 ∠C的大小;作∠B =∠C;则∠B的一条边和∠C的一条边的延长线交于点A.如下图所示:△ABC即为所求
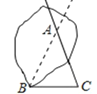
方法2:作边BC的垂直平分线与∠C的另一边的延长线交于点A,连接AB,如下图所示:△ABC即为所求.
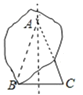
方法3:如图,将长方形纸片对折使点B和点C重合,找到∠ C的另一边的延长线与折痕的交点A,连接AB,如下图所示:△ABC即为所求

(2)证法1:作∠A的平分线AD,交BC与点D
∴∠BAD=∠CAD
在△ABD和△ACD中

∴△ABD≌△ACD
∴AB=AC,
即△ABC为等腰三角形;
证法2:过A作AD⊥BC于D,

∴∠ADB=∠ADC=90°
在△ABD和△ACD中
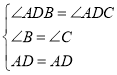
∴△ABD≌△ACD
∴AB=AC,
即△ABC为等腰三角形.

【题目】人寿保险公司的一张关于某地区的生命表的部分摘录如下:
年龄 | 活到该年龄的人数 | 在该年龄的死亡人数 |
40 | 80500 | 892 |
50 | 78009 | 951 |
60 | 69891 | 1200 |
70 | 45502 | 2119 |
80 | 16078 | 2001 |
… | … | … |
根据上表解下列各题:
(1)某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?
(保留三个有效数字)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?