��Ŀ����
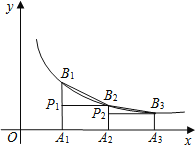
����Ŀ����ͼ,��֪A1,A2,A3,��An,����x���ϵĵ�,��OA1=A1A2=A2A3=��=An1An��=1,�ֱ����A1,A2,A3,��An,����x��Ĵ��߽�����������y=![]() (x>0)��ͼ���ڵ�B1,B2,B3,��,Bn,��,����B2��B2P1��A1B1�ڵ�P1,����B3��B3P2��A2B2�ڵ�P2��,����B1P1B2�����ΪS1,��B2P2B3�����ΪS2��,��BnPnBn+1�����ΪSn.��S1+S2+S3+��+Sn=__.
(x>0)��ͼ���ڵ�B1,B2,B3,��,Bn,��,����B2��B2P1��A1B1�ڵ�P1,����B3��B3P2��A2B2�ڵ�P2��,����B1P1B2�����ΪS1,��B2P2B3�����ΪS2��,��BnPnBn+1�����ΪSn.��S1+S2+S3+��+Sn=__.
���𰸡�![]()
��������
��OA1=A1A2=A2A3=��=An-1An=1��֪B1�������Ϊ��1��y1����B2�������Ϊ��2��y2����B3�������Ϊ��3��y3����Bn�������Ϊ��n��yn������x=1��x=2��x=3���뷴���������Ľ���ʽ�������y1��y2��y3��ֵ�����������ε������ʽ�ɵó�S1��S2��S3��Sn��ֵ���ʿɵó����ۣ�
�⣺��OA1=A1A2=A2A3=��=An-1An=1��
����B1��1��y1����B2��2��y2����B3��3��y3������Bn��n��yn����
��B1��B2��B3��Bn�ڷ���������y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��y1=1��y2=![]() ��y3=
��y3=![]() ��yn=
��yn=![]() ��
��
��S1=![]() ��1����y1-y2��=
��1����y1-y2��=![]() ��1����1-
��1����1-![]() ��=
��=![]() ��1-
��1-![]() ����
����
S2=![]() ��1����y2-y3��=
��1����y2-y3��=![]() ����
����![]() ����
����
S3=![]() ��1����y3-y4��=
��1����y3-y4��=![]() ����
����![]() ����
����
��
Sn=![]() ����
����
��S1+S2+S3+��+Sn=![]() ��1-
��1-![]() +��+
+��+![]() ��=
��=![]() ��
��
�ʴ�Ϊ��![]() ��
��