题目内容
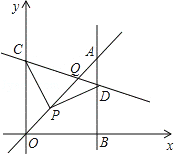
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为______________________
【答案】(![]() ,
, ![]() )
)
【解析】如图:
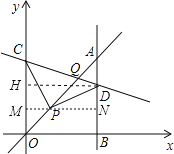
过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
∠CMP=∠DNP=∠CPD=90°,
∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,
∵P(1,1),
∴OM=BN=1,PM=1,
在△MCP和△NPD中,
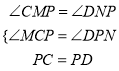
∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,
∵BD=2AD,
∴设AD=a,BD=2a,
∵P(1,1),
∴DN=2a1,
则2a1=1,
a=1,即BD=2.
∵直线y=x,
∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD=![]() ,
,
在Rt△MCP中,由勾股定理得:CM=![]() ,
,
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,
把D(3,2)代入得:k=![]() ,
,
即直线CD的解析式是y=![]() x+3,
x+3,
即方程组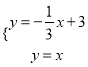 得:
得: ![]() ,
,
即Q的坐标是(![]() ,
, ![]() ),
),
故答案为:(![]() ,
, ![]() )
)

 小学夺冠AB卷系列答案
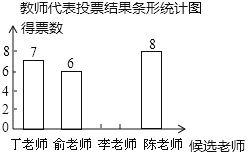
小学夺冠AB卷系列答案【题目】某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表:
候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
得票数 | 200 | 300 |
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?