题目内容
 列分式方程解应用题:
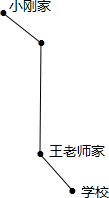
列分式方程解应用题:(1)如图,小刚家、王老师家,学校在同一条路上,小刚家到王老师家的路程为3千米,王老师家到学校的路程为0.5千米.由于小刚的父母战斗在抗“非典”第一线,为了使他能按时到校,王老师每天骑自行车接小刚上学.已知王老师骑自行车的速度是步行的3倍,每天比平时步行上班多用了20分钟,问王老师的步行速度及骑自行车的速度各是多少?
(2)甲、乙两个工程队共同完成一项工程,乙队先单独做1天,再由两队合作2天就完成全部工程,已知甲队与乙队的工作效率之比是3:2,求甲、乙两队单独完成此项工程各需多少天?
分析:(1)是一道有关于行程的问题,注意把握好路程、速度、时间三者的关系.等量关系为:骑自行车接小刚到学校用的时间-平时步行用的时间=多用的时间.
(2)是一道有关工作量的问题,注意工作量=工作时间×工作效率.等量关系为:乙队1天的工作量+甲乙合作2天的工作量=1.
(2)是一道有关工作量的问题,注意工作量=工作时间×工作效率.等量关系为:乙队1天的工作量+甲乙合作2天的工作量=1.
解答:解:(1)设王老师步行的速度是x千米/时,则骑自行车的速度是3x千米/时.
20分钟=
小时.
由题意得:
-
=
.
解得:x=5.
经检验:x=5是原分式方程的解.
∴3x=3×5=15.
答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时.
(2)设甲队单独完成此项工程需2x天,则乙队需要3x天.
由题意得:
+2(
+
)=1.
解得:x=2.
经检验:x=2是原分式方程的解.
∴2x=2×2=4;
3x=3×2=6.
答:甲队单独完成此项工程需4天,乙队单独完成此项工程需6天.
20分钟=
| 1 |
| 3 |
由题意得:
| 6+0.5 |
| 3x |
| 0.5 |
| x |
| 1 |
| 3 |
解得:x=5.
经检验:x=5是原分式方程的解.
∴3x=3×5=15.
答:王老师步行的速度是5千米/时,骑自行车的速度是15千米/时.
(2)设甲队单独完成此项工程需2x天,则乙队需要3x天.
由题意得:
| 1 |
| 3x |
| 1 |
| 3x |
| 1 |
| 2x |
解得:x=2.
经检验:x=2是原分式方程的解.
∴2x=2×2=4;
3x=3×2=6.
答:甲队单独完成此项工程需4天,乙队单独完成此项工程需6天.
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目