题目内容
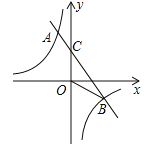
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象相交于A(-1,m),B(n,-1)两点,直线AB与y轴交于C点,连接OB.
的图象相交于A(-1,m),B(n,-1)两点,直线AB与y轴交于C点,连接OB.
(1)求一次函数的表达式;
(2)在x轴上找一点P,连接BP,使△BOP的面积等于△BOC的面积的2倍,求满足条件的点P的坐标.
【答案】(1)y=-x+2;(2)P(12,0)或P(-12,0).
【解析】
(1)先利用反比例函数解析式确定A点和B点坐标,然后利用待定系数法求一次函数解析式;
(2)设P(t,0),先确定C(0,2),再计算出S△OBC=3,则利用题意得到![]() |t|1=6,然后解绝对值方程求出t,从而得到P点坐标.
|t|1=6,然后解绝对值方程求出t,从而得到P点坐标.
(1)把A(﹣1,m),B(n,﹣1)代入y![]() 得:m=3,n=3,∴A(﹣1,3),B(3,﹣1),把A(﹣1,3),B(3,﹣1)代入y=kx+b得:
得:m=3,n=3,∴A(﹣1,3),B(3,﹣1),把A(﹣1,3),B(3,﹣1)代入y=kx+b得:![]() ,解得:
,解得:![]() ,∴一次函数解析式为y=﹣x+2;
,∴一次函数解析式为y=﹣x+2;
(2)设P(t,0),当x=0时,y=﹣x+2=2,则C(0,2),∴S△OBC![]() 2×3=3.
2×3=3.
∵△BOP的面积等于△BOC面积的2倍,∴![]() |t|1=6,∴t=12或t=﹣12,∴P点坐标为(12,0)或(﹣12,0).
|t|1=6,∴t=12或t=﹣12,∴P点坐标为(12,0)或(﹣12,0).

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、和
、和![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.