题目内容
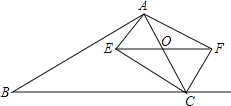
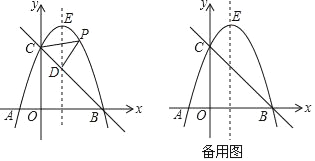
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .以
.以![]() 为顶点,
为顶点,![]() 为一边,在
为一边,在![]() 外部作
外部作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)根据推理可得![]() __________,
__________,![]() __________;(用含
__________;(用含![]() 的代数式表示)
的代数式表示)
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

【答案】(1)证明见解析;(2)![]() ,
,![]() ;(3)
;(3)![]() 为125°或110°或140°.
为125°或110°或140°.
【解析】
(1)根据等边三角形的性质求出![]() ,
,![]() ,然后利用SAS定理证得
,然后利用SAS定理证得![]() ,然后根据全等三角形的和等式的性质可求
,然后根据全等三角形的和等式的性质可求![]() ,
,![]() ,从而判定△OCD是等边三角形,从而求解;
,从而判定△OCD是等边三角形,从而求解;
(2)根据∠AOD=360°-∠AOB-∠BOC-∠COD求解;根据全等三角形的性质可知∠ADC=∠BOC=α,又由等边三角形的性质可得∠ODC=60°,从而求出∠ODA的度数;
(3)分三种情况讨论,利用已知条件及等腰三角形的性质即可求解.
解:(1)![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,
![]() 是等边三角形.
是等边三角形.
![]() .
.
(2)由题意可知:∠AOD=360°-∠AOB-∠BOC-∠COD且![]() ,
,![]()
又由(1)可知![]() 是等边三角形.
是等边三角形.
∴∠COD=60°
∴∠AOD=360°-110°-α-60°=190°-α;
由(1)可知:![]() 且
且![]() 是等边三角形
是等边三角形
∴∠ADC=∠BOC=α且∠ODC=60°
∴∠ADC=∠BOC-∠ODC=α-60°
故答案为:![]() ;
;![]() ;
;
(3)解:①当![]() 时,
时,![]() ,
,
即![]() ,
,
解,得![]() .
.
②当![]() 时,
时,![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
解,得![]() .
.
③当![]() 时,
时,![]() ,
,
即![]() ,
,
解,得![]() .
.
![]() 当
当![]() 为125°或110°或140°时,
为125°或110°或140°时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
相关题目