题目内容
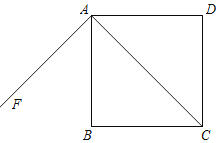
【题目】如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△ABE绕着点A旋转后能与△ADF重合,若AF=5cm,则四边形ABCD的面积为_____.
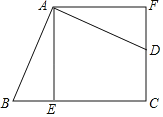
【答案】25cm2
【解析】
根据垂直的定义可得∠AEB=∠AEC=90°,根据旋转变换只改变图形的位置不改变图形的形状与大小可得△ADF和△ABE全等,根据全等三角形对应角相等可得∠AEB=∠F,全等三角形对应边相等可得AE=AF,然后证明四边形是矩形,再根据邻边相等的矩形是正方形可得四边形AECF是正方形,然后根据正方形的面积公式列式计算即可得解.
解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∵AB=AD,△BEA旋转后能与△DFA重合,
∴△ADF≌△ABE,
∴∠AEB=∠F,AE=AF,
∵∠C=90°,
∴∠AEC=∠C=∠F=90°,
∴四边形AECF是矩形,
又∵AE=AF,
∴矩形AECF是正方形,
∵AF=5cm,
∴四边形ABCD的面积=四边形AECF的面积=52=25cm2.
故答案为:25cm2.

练习册系列答案
相关题目