题目内容
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )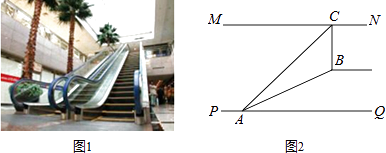
A.10.8米
B.8.9米
C.8.0米
D.5.8米
【答案】D
【解析】解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴ ![]() =
= ![]() =
= ![]() .
.
设BD=5k(米),AD=12k(米),则AB=13k(米).
∵AB=13(米),
∴k=1,
∴BD=5(米),AD=12(米).
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=ADtan∠CAD≈12×0.90≈10.8(米),
∴BC=10.8﹣5≈5.8(米).
故选:D.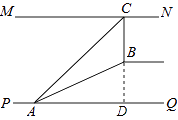
【考点精析】本题主要考查了关于坡度坡角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA才能正确解答此题.

【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 (汇款不足100元时按100元汇款收汇费) |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 (汇款不足100元的部分不收汇费) |
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.