Question

【题目】如图，ABCD是直角梯形，AB=18cm，CD=15cm，AD=6cm，点P从B点开始，沿BA边向点A以1cm/s的速度移动，点Q从D点开始，沿DC边向点C以2cm/s的速度移动，如果P、Q分别从B、D同时出发，P、Q有一点到达终点时运动停止，设移动时间为t．

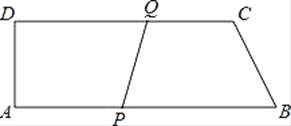
（1）t为何值时四边形PQCB是平行四边形？

（2）t为何值时四边形PQCB是矩形？

（3）t为何值时四边形PQCB是等腰梯形？

Answer 1

【答案】（1）当t=5时，四边形PQCB是平行四边形；（2）BC与AB不垂直，所以PQCB不可能是矩形；（3）当t=7时，四边形PQCB是菱形.

【解析】

（1）若四边形PQCB是平行四边形，则QC=PB，即DC-2t=t，求出t的值即可；
（2）由于BC与AB不垂直，所以无论t为何值，四边形PQCB都不可能是矩形；
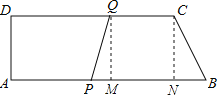
（3）分别过点Q、C作QM⊥AB、CN⊥AB，由于梯形ABCD是直角梯形，故四边形AMQD是矩形，BN=AB-CD，
因为四边形PQCB是等腰梯形，故PM=BN，由此即可得出t的值．

解：

（1）∵四边形PQCB是平行四边形，
∴QC=PB，即DC-2t=t，
∴15-2t=t，解得t=5；

（2）∵BC与AB不垂直，
∴无论t为何值，四边形PQCB都不可能是矩形；

（3）分别过点Q、C作QM⊥AB、CN⊥AB，
∵梯形ABCD是直角梯形，AB=18cm，CD=15cm
∴四边形AMQD是矩形，BN=AB-CD=18-15=3cm，
∵四边形PQCB是等腰梯形，
∴PM=BN=3cm，
∴DQ=BP-PM，即2t=18-t+3，解得t=7（秒）．