题目内容
(2011•红桥区一模)已知函数y1=x,y2=
x2+
.
(Ⅰ)当自变量x=1时,分别计算函数y1、y2的值;
(Ⅱ)说明:对于自变量x的同一个值,均有y1≤y2成立;
(Ⅲ)是否存在二次函数y3=ax2+bx+c同时满足下列两个条件:
①当x=-1时,函数值y1≤y3≤y2; ②对于任意的实数x的同一个值,都有y1≤y3≤y2,
若存在,求出满足条件的函数y3的解析式;若不存在,请说明理由.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)当自变量x=1时,分别计算函数y1、y2的值;
(Ⅱ)说明:对于自变量x的同一个值,均有y1≤y2成立;
(Ⅲ)是否存在二次函数y3=ax2+bx+c同时满足下列两个条件:
①当x=-1时,函数值y1≤y3≤y2; ②对于任意的实数x的同一个值,都有y1≤y3≤y2,
若存在,求出满足条件的函数y3的解析式;若不存在,请说明理由.
分析:(1)自己把x=1分别代入两个函数的解析式中计算即可求解;
(2)首先利用y1-y2,然后利用配方法证明y1-y2≤0即可求解;
(3)首先假设存在y3=ax2+bx+c,使得y1≤y3≤y2成立,由于当x=-1时,y3=0,而y1=-1,y2=1,由此得到a-b+c=0,又当x=1时,1≤a+b+c≤1,由此得到a+b+c=1,所以b=a+c=
,进一步得到y3=ax2+(a+c)x+c,当x≤ax2+(a+c)x+c,即0≤ax2+(a+c-1)x+c,若ax2+(a+c)x+c≤
x2+
,即(a-
)x2+(a+c)x+(c-
)≤0,由此可以分别得到两个不等式组,解不等式组并且讨论即可解决问题.
(2)首先利用y1-y2,然后利用配方法证明y1-y2≤0即可求解;
(3)首先假设存在y3=ax2+bx+c,使得y1≤y3≤y2成立,由于当x=-1时,y3=0,而y1=-1,y2=1,由此得到a-b+c=0,又当x=1时,1≤a+b+c≤1,由此得到a+b+c=1,所以b=a+c=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)当x=1时,y1=1,y2=1;
(2)y1-y2=x-(
x2+
)
=-
x2+x-
=-
(x2-2x+1)
=-
(x-1)2≤0,
∴y1≤y2;
(3)假设存在y3=ax2+bx+c,使得y1≤y3≤y2成立,
当x=-1时,y3=0,y1=-1,y2=1,
∴a-b+c=0,
当x=1时,1≤a+b+c≤1,
∴a+b+c=1,
∴b=a+c=
,
∴y3=ax2+(a+c)x+c,
若x≤ax2+(a+c)x+c,即0≤ax2+(a+c-1)x+c
得
,即
①
若ax2+(a+c)x+c≤
x2+
,即(a-
)x2+(a+c)x+(c-
)≤0
得
,即
由不等式①、②得:0<a<
,(a-c)2≤0,a=c=
,
∴满足条件的函数解析式为y3=
x2+
x+
.
(2)y1-y2=x-(
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
=-
| 1 |
| 2 |
∴y1≤y2;
(3)假设存在y3=ax2+bx+c,使得y1≤y3≤y2成立,
当x=-1时,y3=0,y1=-1,y2=1,
∴a-b+c=0,
当x=1时,1≤a+b+c≤1,
∴a+b+c=1,
∴b=a+c=
| 1 |
| 2 |
∴y3=ax2+(a+c)x+c,
若x≤ax2+(a+c)x+c,即0≤ax2+(a+c-1)x+c
得
|
|
若ax2+(a+c)x+c≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得
|
|
由不等式①、②得:0<a<
| 1 |
| 2 |
| 1 |
| 4 |
∴满足条件的函数解析式为y3=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题考查了二次函数的综合题,其中涉及到的知识点有求二次函数的函数值和函数值的大小的比较.在求有关开放性问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
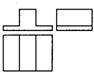 (2011•红桥区一模)右面的三视图对应的物体是( )
(2011•红桥区一模)右面的三视图对应的物体是( )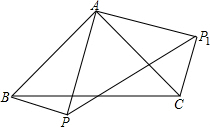 (2011•红桥区一模)如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后能与△ACP1重合.若AP=3,则PP1的长是
(2011•红桥区一模)如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后能与△ACP1重合.若AP=3,则PP1的长是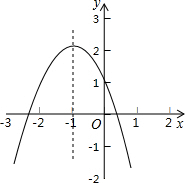 (2011•红桥区一模)已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:(1)a+b+c<0;(2)a+b+c>0;(3)abc>0;(4)4a-2b+c<0;(5)c-a>1,其中正确的是( )
(2011•红桥区一模)已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:(1)a+b+c<0;(2)a+b+c>0;(3)abc>0;(4)4a-2b+c<0;(5)c-a>1,其中正确的是( )