题目内容
【题目】如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥x轴于N,把△AND沿直线AB翻折,得到△AMD,延长MA交y轴于点C,过A、C、D三点的圆E与x轴交于点F,连结DF. 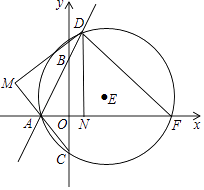
(1)直接写出tan∠BAO的值为;
(2)求证:MC=NF;
(3)求线段OC的长;
(4)是否存在点D,使DF∥AC?若存在,求点D的坐标;若不存在,请说明理由.
【答案】
(1)2
(2)解:连接DC,则∠MCD=∠NFD,
在△MCD与△DNF中, 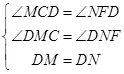 ,
,
∴△MCD≌△NFD,
∴MC=NF;
(3)解:作CG⊥y轴于G,
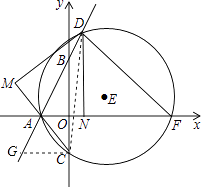
∵CG∥x轴,
∴∠AGC=∠DAF,
∵∠GAC=∠MAD=∠DAF,
∴∠AGC=∠GAC,
∴GC=AC,
设GC=a,
∵tan∠BAO=tan∠BGC=2,
∴BC=2a,
∴OC=2a﹣3,
∵AO2+OC2=AC2,
∴1.52+(2a﹣3)2=a2,
解得:a= ![]() ,a=
,a= ![]() (舍去),
(舍去),
∴线段OC的长是2;
(4)解:存在,理由:设D(m,2m+3)
当DF∥AC时,∠DFA=∠FAC,
由(3)知,tan∠CAO= ![]() ,
,
∴tan∠DFA= ![]() ,
,
∵DN=2m+3,
∴NF= ![]() (2m+3),
(2m+3),
∵MA=AN= ![]() +m,AC=
+m,AC= ![]() =
= ![]() ,
,
∴NF=MC=AC+AM= ![]() +m+
+m+ ![]() =4+m=
=4+m= ![]() (2m+3),
(2m+3),
解得:m= ![]() ,
,
∴存在点D( ![]() ,10).
,10).
【解析】解:(1)在y=2x+3中,令y=0,得x=﹣ ![]() ,令x=0,得y=3, ∴A(﹣
,令x=0,得y=3, ∴A(﹣ ![]() ,0),B(0,3),
,0),B(0,3),
∴OA= ![]() ,OB=3,
,OB=3,
∴tan∠BAO= ![]() =2;
=2;
所以答案是:2;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目