��Ŀ����
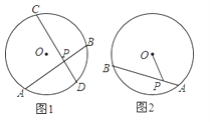
����Ŀ�����꼶ѧ��С����һ��ϲ������ĺ�ѧ��������ѧϰ��ڶ�ʮ����Բ���ڼ���ͻȻ�����ְֵij�����ѧ���Ͼ�Ȼ����һ���ཻ�Ҷ�����Բ�ڵ������ཻ�ң�������ֳɵ������߶γ��Ļ���ȣ����dz����棬��ϸ�Ķ�ԭ�����ǣ�PAPB=PCPD��С�պ���֪�������֤���ģ�����֤�������������ˣ�ֻ���������ߵ��������ֱ�����AC��BD����������һ���ܰ���֤��������ͼ1�����������ߣ���д����ϸ��֤�����̣�
С���ֿ���һ���κ�ϰ�⣬��ͼ2��AB�ǡ�O�ң�P��AB��һ�㣬AB=10cm��PA=4cm��OP=5cm�����O�İ뾶�����С�գ��������˵���϶������������д����ϸ��֤�����̣�
���𰸡���1������������2����O�İ뾶RΪ7��
��������
��1������AC��BD������Բ�ܽǶ����õ���C=��B����A=��D���ٸ������������Ƶ��ж������õ���APC�ס�DPB���������������ε����ʵ�AP��DP=CP��BP��������APBP=CPDP���ɴ˵õ��ཻ�Ҷ�����
��2����AB=10��PA=4��OP=5����PB=10-4=6��PC=OC-OP=R-5��PD=OD+OP=R+5�������ཻ�Ҷ����õ�PAPB=PCPD����4��6=��R-5������R+5�����ⷽ�̼��ɵõ�R��ֵ��
��1��Բ���������ཻ���������ұ�����ֳɵ������߶εĻ���ȣ�
��֪����ͼ1����O������AB��CD�ཻ��E��
��֤��APBP=CPDP��
֤�����£�
����AC��BD����ͼ1��
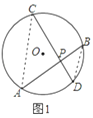
�ߡ�C=��B����A=��D��
���APC�ס�DPB��
��AP��DP=CP��BP��
��APBP=CPDP��
�����������ཻ��������ֳɵ������߶εĻ���ȣ�
��2����P��ֱ��CD����ͼ2��
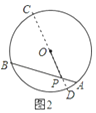
��AB=10��PA=4��OP=5��
��PB=10��4=6��PC=OC��OP=R��5��PD=OD+OP=R+5��
�ɣ�1���н��۵ã�PAPB=PCPD��
��4��6=��R��5������R+5����
���R=7��R=��7��ȥ����
���ԡ�O�İ뾶R=7��