题目内容
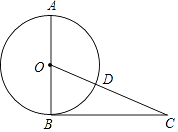
【题目】如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD= ![]() AC,AB=8,E是AB上任意一点,F是AC上任意一点,则折线DEFB的最短长度为 .
AC,AB=8,E是AB上任意一点,F是AC上任意一点,则折线DEFB的最短长度为 . 
【答案】![]()
【解析】解:作D点关于AB的对称点D′,B点关于AC的对称点B′,连接D′B′分别交AB于点E,AC于点F,作B′R⊥AB,
过点D′作D′W⊥B′R于点W,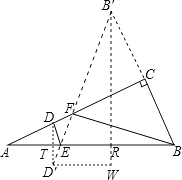
∵∠CAB=30°,∠C=90°.AD= ![]() AC,AB=8,
AC,AB=8,
∴BC=4,AC=4 ![]() ,则AD=
,则AD= ![]() ,BB′=8,B′R=4
,BB′=8,B′R=4 ![]() ,
,
∴DT= ![]() AD=
AD= ![]() ,AT=
,AT= ![]() =
= ![]() ,BR=4,
,BR=4,
∴RW= ![]() ,D′W=8﹣
,D′W=8﹣ ![]() ﹣4=
﹣4= ![]() ,
,
∴B′W= ![]() ,
,
B′D′= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用轴对称-最短路线问题的相关知识可以得到问题的答案,需要掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目