题目内容
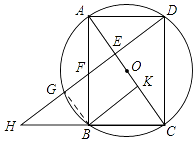
【题目】已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点. 
(1)求证:点D在⊙O上;
(2)求证:F是AB的中点;
(3)若DE=4,求⊙O的半径和△BFH的面积.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AO=OC=OD=OB,
∵以O为圆心,OA长为半径作⊙O,
∴点D在⊙O上;
(2)证明:同理,点B也是⊙O上,
连接BG,
∵∠BAD=90°,
∴BD也是直径,
∴∠BGD=90°,
∵BK⊥AC,BK∥DH,
∴∠GEK=90°,
∴BG∥AC,
∴∠FAE=∠FBG,
∵F是EG的中点,
∴EF=FG,
∵∠AFE=∠BFG,
∴△AEF≌△BGF,
∴AF=BF,
∴F是AB的中点;
(3)证明:由(2)得:△AEF≌△BGF,
∴AE=BG,
∵OE⊥DG,
∴DE=EG=4,
∵OB=OD,
∴OE是△DGB的中位线,
∴OE= ![]() BG,
BG,
∴OE= ![]() AE,
AE,
设OE=x,则AE=2x,
∴OD=3x,
在Rt△OED中,由勾股定理得:OE2+ED2=OD2,
∴x2+42=(3x)2,
x= ![]() ,
,
∴OD=3 ![]() ,即⊙O的半径为3
,即⊙O的半径为3 ![]() ;
;
Rt△AED中,AE=2 ![]() ,ED=4,
,ED=4,
∴AD= ![]() =2
=2 ![]() ,
,
Rt△ABD中,BD=2OD=6 ![]() ,
,
AB= ![]() =4
=4 ![]() ,
,
∵AF=BF,∠AFD=∠BFH,∠DAF=∠ABH=90°,
∴△AFD≌△BFH,
∴BH=AD=2 ![]() ,
,
BF=AF= ![]() AB=2
AB=2 ![]() ,
,
∴S△BFH= ![]() BFBH=
BFBH= ![]() ×
× ![]() =6
=6 ![]() .
.
【解析】(1)根据矩形的对角线相等且平分的性质得:OA=OD,所以点D在⊙O上;(2)证明△AEF≌△BGF,则AF=BF;(3)先在Rt△OED中,由勾股定理求⊙O的半径为3 ![]() ;再利用勾股定理计算AD=
;再利用勾股定理计算AD= ![]() =2
=2 ![]() , AB=
, AB= ![]() =4
=4 ![]() ,证明△AFD≌△BFH,可得S△BFH=
,证明△AFD≌△BFH,可得S△BFH= ![]() BFBH,代入计算即可.
BFBH,代入计算即可.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案






