题目内容
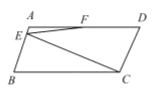
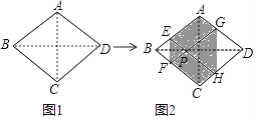
【题目】如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM,过E作EF⊥AM垂足为F,EF交DC于点N.

(1)求证:AF=BM;
(2)若AB=12,AF=5,求DE的长.
【答案】(1)见解析;(2)DE=1.
【解析】
(1)由正方形的性质和已知可得∠ABC=∠AFE=90°,由AD∥BC得∠AMB=∠EAF,根据“AAS”可证△ABM≌△EFA,可得AF=BM;
(2)由勾股定理可求AM=13,由全等三角形的性质可得AM=AE=13,即可求DE的长.
(1)证明:∵四边形ABCD是正方形
∴∠ABC=90°,AD∥BC
∴∠EAF=∠AMB,
∵EF⊥AM,
∴∠AFE=∠ABC=90°,
在△ABM和△EFA中,
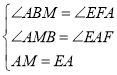 ,
,
∴△ABM≌△EFA(AAS)
∴AF=BM;
(2)解:∵AF=5,
∴BM=AF =5,
在Rt△ABM中,AB=12, BM=5,
∴AM=![]() ,
,
∴AE =AM= 13,
∵四边形ABCD是正方形,
∴AD =AB=12,
∴DE=AEAD=1312=1.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.