题目内容
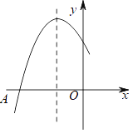
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )
A. ②④ B. ①④ C. ①③ D. ②③
【答案】B
【解析】
①根据抛物线与x轴交点个数可判断;②根据抛物线对称轴可判断;③根据抛物线与x轴的另一个交点坐标可判断;④根据两点离对称轴远近可判断.
解:由函数图象可知抛物线与x轴有2个交点,
∴b2-4ac>0即b2>4ac,故①正确;
∵对称轴为直线x=-2,
∴-![]() =-2,即4a-b=0,故②错误;
=-2,即4a-b=0,故②错误;
∵抛物线与x轴的交点A坐标为(-5,0)且对称轴为x=-2,
∴抛物线与x轴的另一交点为(1,0),故③错误;
∵对称轴为x=-2,开口向下,
∴点(-4,y1)比点(-1,y2)离对称轴远,
∴y1<y2,故④正确;
综上,正确的结论是:①④,
故选:B.

练习册系列答案
相关题目
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁