题目内容
【题目】在梯形ABCD中,AD∥BC , AB=CD , ∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由 . 
【答案】解:△EFG为等边三角形;证明如下:
如图,连接DE、CF;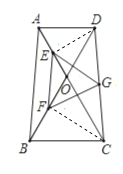
∵AD∥BC , AB=CD ,
∴四边形ABCD为等腰梯形,
∴AC=BD;
在△ABD与△DCA中,
AB=DC
AD=DA
BD=AC
∴△ABD≌△DCA(SSS),
∴∠OAD=∠ODA , AO=DO;而∠AOD=60°,
∴△AOD为等边三角形,AD=OD;
∵AE=OE ,
∴DE⊥AO , △CDE为直角三角形,
∵DG=CG ,
∴EG= ![]() CD;同理可求:FG=
CD;同理可求:FG= ![]() CD;
CD;
∵E为OA的中点,F为OB的中点,
∴EF为△OAB的中位线,
∴EF= ![]() AB;而AB=CD ,
AB;而AB=CD ,
∴EG=FG=EF ,
∴△EFG为等边三角形 .
【解析】如图,作辅助线;首先证明∠OAD=∠ODA , 得到AO=DO , 结合∠AOD=60°,判断出△AOD为等边三角形,此为解题的关键性结论;其次证明DE⊥AC , 运用直角三角形的性质证明EG=FG= ![]() CD;运用三角形的中位线定理证明EF=
CD;运用三角形的中位线定理证明EF= ![]() AB , 结合AB=CD , 得到EG=FG=EF , 即可解决问题 .
AB , 结合AB=CD , 得到EG=FG=EF , 即可解决问题 .
【考点精析】利用三角形中位线定理对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
相关题目