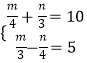题目内容
【题目】若不等式组  ,的整数解是关于x的方程2x-4=ax的根,求a的值.
,的整数解是关于x的方程2x-4=ax的根,求a的值.
【答案】解:解不等式2 x+ 3 < 1,得x<-1;
解不等式x > ![]() ( x- 3 ) ,得x>-3,
( x- 3 ) ,得x>-3,
则不等式组的解集为-3<x<-1,
则不等式组的整数解为-2.
把x=-2代入2x-4=ax,得-4-4=-2a,解得a=4.
【解析】解出不等式组的解集,找出其中的整数解,再将x的整数解代入方程解出a即可.
【考点精析】掌握解一元一次方程的步骤和一元一次不等式组的解法是解答本题的根本,需要知道先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).

练习册系列答案
相关题目
【题目】九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队