题目内容
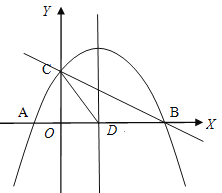
【题目】如图,抛物线![]() 与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
(1)求抛物线的解析式;
(2)求sin∠ABC的值;
(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
【答案】(1)解析式为![]() ;
;
(2)![]() ;
;
(3)存在,点P的坐标为(![]() ,
, ![]() )、(
)、(![]() ,4)或(
,4)或(![]() ,-
,-![]() ).
).
(4)当点E坐标为(2,1)时,线段EF最长.
【解析】试题分析: (1)把A(-1,0),C(0,2)代入y=-![]() x2+bx+c列方程组即可.
x2+bx+c列方程组即可.
(2)令y=0,求出x的值,可确定点B的坐标,然后由点B、C的坐标,利用勾股定理可求出BC的长,即可求sin∠ABC的值;
(3)由勾股定理求出CD的值,再以点C为圆心,CD为半径作弧交对称轴于P1,以点D为圆心CD为半径作圆交对称轴于点P2,P3,作CE垂直于对称轴与点E,由等腰三角形的性质及勾股定理就可以求出结论;
(4)设出E点的坐标为(x,-![]() x+2),就可以表示出F的坐标,进而求出EF的长,由二次函数的性质可求出答案.
x+2),就可以表示出F的坐标,进而求出EF的长,由二次函数的性质可求出答案.
试题解析:(1)∵抛物线![]() 过点A(-1,0),C(0,2),
过点A(-1,0),C(0,2),

∴b=![]() ,c=2.
,c=2.
∴解析式为![]() .
.
(2)∵点B的坐标为(4,0),
∴BC=![]() .
.
![]() .
.
(3)存在.
∵点D的坐标为(![]() ,0),
,0),
![]() .
.
∴点P的坐标为(![]() ,
, ![]() )、(
)、(![]() ,4)或(
,4)或(![]() ,-
,- ![]() ).
).
(4)设直线BC的解析式为![]()
∵B、C两点坐标分别为(4,0)、(0,2),
∴4m+n=0,n=2,
∴m=![]() ,n=2
,n=2
∴直线BC的解析式为![]() .
.
设E点坐标为![]() ,则F点坐标为
,则F点坐标为![]()
![]()
∴当点E坐标为(2,1)时,线段EF最长.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案