题目内容
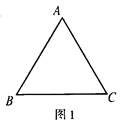
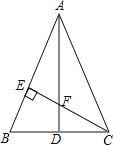
【题目】如图,△ABC中,AB=AC,作AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE相交于点F,若已知AE=CE.
(1)求证:△AEF≌△CEB;
(2)求证:AF=2CD
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)要证明△AEF≌△CEB,已知条件有AE=EC,∠AEF=∠BEC=90°,还差一个条件,由AD⊥BC,CE⊥AB可得∠B+∠BAD=90°,∠B+∠BCE=90°,所以得出∠EAF=∠ECB,因此可证明出△AEF≌△CEB;(2)由(1)结论可得:AF=BC,即要证明BC=2CD,由等腰三角形三线合一性质不难证明.
试题解析:
(1)证明:∵AD⊥BC,
∴∠B+∠BAD=90°,
∵CE⊥AB,
∴∠B+∠BCE=90°,
∴∠EAF=∠ECB,
在△AEF和△CEB中,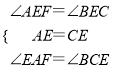 ,
,
∴△AEF≌△CEB;
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴CD=BD,BC=2CD,
∴AF=2CD.

练习册系列答案
相关题目