��Ŀ����
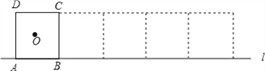
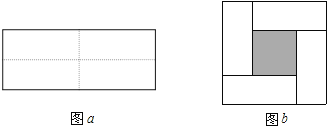
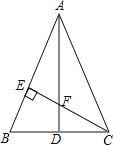
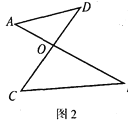
����Ŀ����ͼ��ͼ1�ǡ�ABC��ͼ2�ǡ�8���Ρ������߶�AB��CD�ཻ�ڵ�O������AD��CB�γɵ�ͼ�Σ���ͼ3��һ���������״���Խ���������⣺
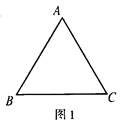

(1)ͼ1�ġ�ABC�У���A����B����C��_____����֤����д���Ľ��ۣ���Ҫ������֤�����̣�
(2)ͼ2�ġ�8���Ρ��У���ֱ��д����A����B����C����D֮���������ϵ��_____��
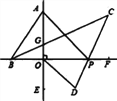
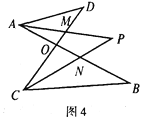
(3)����ͼ2�������£�����DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N(��ͼ4)����ֱ��д����P���D����B֮��������ϵ��____��
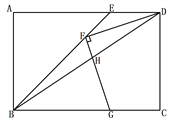
(4)ͼ3�еĵ�A�����Ƶ��߶�BE��ʱ����ֱ��д����CAD����B����C����D����E��____��
���𰸡� 180�� ��A+��D=��C+��B ��P=![]() ����D+��B�� 180��
����D+��B�� 180��
�������������������1���ȹ�A����EF��BC��������ֱ��ƽ�У��ڴ�����ȵó���B=��EAB����C=��CAF���ٸ��ݡ�EAB+��A+��CAF=180�㣬����֤����A+��B+��C�Ķ�����
��2�������������ڽǺͶ������ɵó���A+��D=��C+��B��
��3�����ݽ�ƽ���ߵ����ʵó���1=��2����3=��4���ٸ��ݶԶ��ǵ����ʣ��ó���1+��D=��3+��P����2+��P=��4+��B�����ɵó���D-��P=��P-��B���������������ɣ�
��4�����������ڽ�֮�͵��ں��������ڵ�һ����ǵó���CAD+��D=��CFG����B+��E=��CGF���ٸ����������ڽǺͶ��������ɵó��𰸣�
�����������1����A����EF��BC��
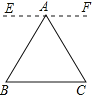
��EF��BC��
���B=��EAB����C=��CAF��
�ߡ�EAB+��A+��CAF=180�㣬
���A+��B+��C=180�㣻
��2���ߡ�A+��D+��AOD=��C+��B+��BOC=180�㣬
�֡ߡ�AOD=��BOC���Զ�����ȣ���
���A+��D=��C+��B��
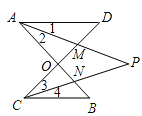
��3����AP��CP�ǡ�DAB����BCD��ƽ���ߣ�
���1=��2����3=��4��
�ߡ�1+��D=��3+��P����2+��P=��4+��B��
���D-��P=��P-��B��
���P=![]() ����D+��B����
����D+��B����
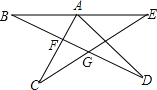
��4���ߡ�CAD+��D=��CFG����B+��E=��CGF��
�֡ߡ�C+��CFG+��CGF=180�㣬
���CAD+��B+��C+��D+��E=180�㣻

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�