题目内容
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.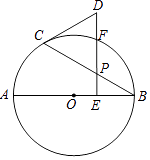
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
【答案】
(1)证明:连接OC,

∵DP=DC,
∴∠DPC=∠DCP,
∵∠DPC=∠BPE,
∴∠BPE=∠DCP,
∵PE⊥AB,
∴∠BEP=90°,
∴∠B+∠APE=90°,
∵OB=OC,
∴∠OCB=∠B,
∴∠OCB+∠DCP=90°,
∴OC⊥CD,
∴直线CD与⊙O相切
(2)解:以B、O、C、F为顶点的四边形是菱形,理由如下:
连接AC,
∵∠CBA=30°,
∴∠A=60°,
∴△OAC为等边三角形,
∴∠BOC=120°,
连接OF,BF,CF
∵F是弧BC的中点,
∴∠BOF=∠COF=60°,
∴△BOF与△COF均为等边三角形,
∴BF=BO=OC=CF,
∴四边形BOCF为菱形.
【解析】(1)连接OC,然后依据已知条件和圆的基本性质证明OC⊥CD,最后,依据切线的判定定理进行证明即可;
(2)连接AC,由∠CAB=30°可证明△OAC为等边三角形,于是可得到∠BOC=120°,由F是弧AC的中点,易证明△BOF、△COF均为等边三角形,依据等边三角形的性质可得到BF=BO=OC=CF,从而可证明四边形BOCF为菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
相关题目







