题目内容
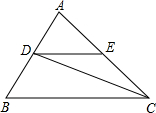
如图所示,E为□ABCD的边AD上的一点,且AE∶ED=3∶2,CE交BD于F,则BF∶FD ( )


| A.3∶5 | B.5∶3 | C.2∶5 | D.5∶2 |
C.
试题分析:由在?ABCD中,且BE:EC=2:3,易得BE:AD=2:5,△ADF∽△EBF,然后根据相似三角形的对应边成比例,即可求得答案.
∵BE:EC=2:3,
∴BE:BC=2:5,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴BE:AD=2:5,△ADF∽△EBF,
∴
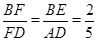 .
.故选C.
考点: 1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
相关题目
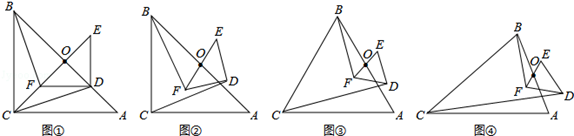
 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)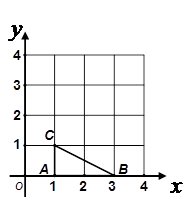
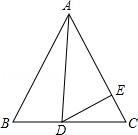

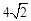 ,则EF+CF的长为( )
,则EF+CF的长为( )