题目内容
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( ) 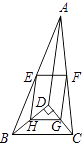
A.7
B.9
C.10
D.11
【答案】D
【解析】解:∵BD⊥DC,BD=4,CD=3,由勾股定理得:BC= ![]() =5, ∵E、F、G、H分别是AB、AC、CD、BD的中点,
=5, ∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG= ![]() BC=EF,EH=FG=
BC=EF,EH=FG= ![]() AD,
AD,
∵AD=6,
∴EF=HG=2.5,EH=GF=3,
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
故选D.
根据勾股定理求出BC的长,根据三角形的中位线定理得到HG= ![]() BC=EF,EH=FG=
BC=EF,EH=FG= ![]() AD,求出EF、HG、EH、FG的长,代入即可求出四边形EFGH的周长.
AD,求出EF、HG、EH、FG的长,代入即可求出四边形EFGH的周长.

练习册系列答案
相关题目