题目内容
【题目】如图,△ABC中,AD为BC边上的中线,若AB=5,AC=13,AD=6,那么BC的值为( ) 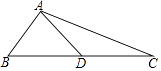
A.18
B.![]()
C.2 ![]()
D.12
【答案】C
【解析】证明:延长AD到点E,使DE=AD=6,连接CE, 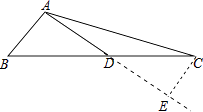
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,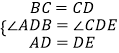 ,
,
∴△ABD≌△CED(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2 ,
∴∠CED=90°,
∴∠BAD=90°,
∴BD2=AB2+AD2 ,
∴BD= ![]() ,
,
∴BC=2BD=2 ![]() ,
,
故选C.
【考点精析】根据题目的已知条件,利用勾股定理的逆定理的相关知识可以得到问题的答案,需要掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目